Was ist I/Q Data?
Übersicht
Vereinfacht gesagt, I/Q-Daten zeigen die Veränderungen in der Größe (oder Amplitude) und Phase einer Neunwelle. Wenn Amplituden- und Phasenänderungen in einer geordneten, vorbestimmten Art und Weise auftreten, können Sie diese Amplituden- und Phasenänderungen verwenden, um Informationen auf einer Neun-Welle zu kodieren, einem Prozess, der als Modulation bekannt ist.
Die Modulation ändert ein höheres Frequenzträgersignal im Verhältnis zu einer niedrigeren Frequenzmeldung oder einem Informationssignal. I/Q-Daten sind in HF-Kommunikationssystemen weit verbreitet, und im Allgemeinen in der Signalmodulation, da es eine bequeme Möglichkeit ist, Signale zu modulieren.
1. Hintergrund Signale
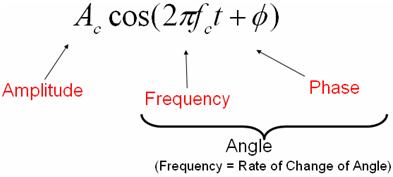
Die Signalmodulation ändert eine Neunwelle, um Informationen zu kodieren. Die Gleichung, die eine Neunwelle darstellt, ist wie folgt:
Bild 1: Gleichung für eine Sinkenwelle
Die darüber hinaus zeigt, dass Sie sich darauf beschränken, Änderungen an der Amplitude, der Häufigkeit und der Phase einer Neunwelle vorzunehmen, um Informationen zu kodieren. Frequenz ist einfach die Veränderungsrate der Phase einer Neunwelle (Frequenz ist das erste Derivat der Phase), so dass Frequenz und Phase der Neun-Wellen-Gleichung gemeinsam als Phasenwinkel bezeichnet werden können. Daher können wir den augenblicklichen Zustand einer Neunwelle mit Vektor in der komplexen Ebene mit Amplitude (Magnitude) und Phasenkoordinaten in einem polaren Koordinatensystem darstellen.
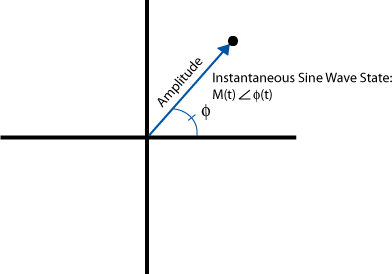
Abbildung 2. Polar Darstellung einer Sinkenwelle
In der Grafik oben stellt die Entfernung vom Ursprung zum Schwarzen die Amplitude (Magnitude) der Sinuswelle dar, und der Winkel von der horizontalen Achse zur Linie stellt die Phase dar. So bleibt die Entfernung vom Ursprung bis zum Punkt gleich, solange sich die Amplitude der Sinuswelle nicht ändert (modulierend). Die Phase des Punktes ändert sich je nach dem aktuellen Zustand der Sinuswelle. Zum Beispiel dreht sich eine Sinuswelle mit einer Frequenz von 1 Hz (2 - Radians/Sekunde) gegen den Ursprung mit einer Geschwindigkeit von einer Umdrehung pro Sekunde um den Ursprung. Wenn sich die Amplitude während einer Revolution nicht ändert, bildet der Punkt einen Kreis um den Ursprung mit Radius, der der Amplitude entspricht, entlang der Punkt mit einer Geschwindigkeit von einem Zyklus pro Sekunde.
Da Phase eine relative Messung ist, stellen Sie sich vor, dass die verwendete Phasenreferenz eine sine Frequenzwelle ist, die der Neunwelle entspricht, die durch die Amplitude und die Phasenpunkte dargestellt wird. Wenn die Referenz-Sine-Wellenfrequenz und die gezeichnete Neunwellenfrequenz gleich sind, ist die Änderungsrate der Phase der beiden Signale gleich, und die Rotation der Sine-Welle um den Ursprung wird stationär. In diesem Fall kann ein einziger Amplituden-/Phasenpunkt eine sine Frequenzwelle darstellen, die der Referenzfrequenz entspricht. Jede Phasendrehung um den Ursprung zeigt einen Frequenzunterschied zwischen der Referenz-Sine-Welle und der gezeichneten Neun-Welle an.
Bis zu diesem Punkt hat dieses Whitepaper Amplituden- und Phasendaten in einem polaren Koordinatensystem beschrieben. Alle oben besprochenen Konzepte gelten für I/Q-Daten. Tatsächlich sind I/Q-Daten nur eine Übersetzung von Amplituden- und Phasendaten aus einem polaren Koordinatensystem in ein kartesische (X,Y) Koordinatensystem. Mit der Trigonometrie können Sie die polaren Koordinaten-Sine-Wellen-Informationen in die karäkischen I/Q-Sine-Wellendaten umwandeln. Diese beiden Darstellungen sind gleichwertig und enthalten die gleichen Informationen, nur in verschiedenen Formen. Diese Äquivalenz zeigt sich in Abbildung 3.
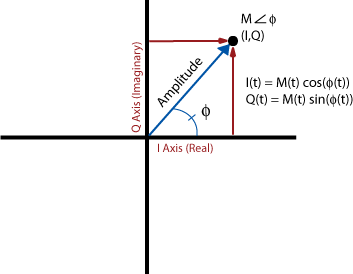
Abbildung 3. I und Q in Polarform
Die Abbildung unten zeigt ein LabVIEW-Beispiel, das die Beziehung zwischen polaren und kartesischen Koordinaten zeigt.
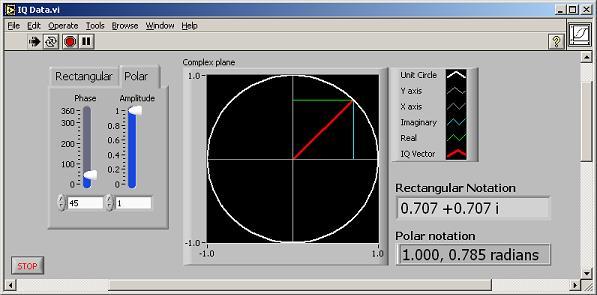
Abbildung 4: I/Q Daten in LabVIEW
2. I/Q Daten in Kommunikationssystemen
Um zu erklären, warum I/Q-Daten in Kommunikationssystemen verwendet werden, müssen Sie die Modulationsgrundlagen verstehen.
HF-Kommunikationssysteme verwenden erweiterte Modulationsformen, um die Datenmenge zu erhöhen, die in einem bestimmten Frequenzspektrum übertragen werden kann. Die Signalmodulation lässt sich in zwei große Kategorien einteilen: analoge Modulation und digitale Modulation. Analog oder Digital bezieht sich auf die Modulation der Daten. Wenn analoge Audiodaten auf einer Träger-Sine-Welle moduliert werden, wird diese Technologie als analoge Modulation bezeichnet. Wenn analoge Audiodaten von einem Analog-Digital-Wandler (ADC) mit den resultierenden digitalen Bits auf einer Kanalsinewelle abgetastet werden, wird diese Technologie als digitale Modulation definiert, da digitale Daten codiert werden. Sowohl analoge Modulation als auch digitale Modulation beinhalten die Änderung der Trägerwellenamplitude, -frequenz oder Phase (oder Kombination von Amplitude und Phase gleichzeitig) gemäß den Nachrichtendaten.
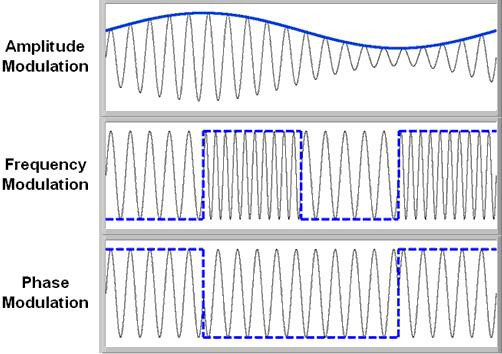
Amplitude Modulation (AM), Frequenzmodulation (FM) oder Phasenmodulation (PM) sind Beispiele für analoge Modulation. Mit der Amplitudenmodulation wird die Träger-Sine-Wellen-Amplitude nach dem Signal moduliert. Die gleiche Idee gilt für Frequenz- und Phasenmodulation.
Abbildung 5. Zeit Domäne von AM, FM und PM Signalen
Abbildung 5 stellt verschiedene analoge Techniken dar - AM, FM und PM - auf ein Trägersignal angewendet. Für AM ist das Nachrichtensignal die blaue Neunwelle, die die "Hülle" der höherfrequenten Träger-Sine-Welle bildet. Für FM sind die Nachrichtendaten die gestrichelte Quadratwelle. Wie die Abbildung zeigt, ändert sich das resultierende Trägersignal zwischen zwei unterschiedlichen Frequenzzuständen. Jeder Frequenzzustand stellt den hohen und niedrigen Zustand des Signalsignals dar. Wenn das Nachrichtensignal in diesem Fall eine Neunwelle wäre, gäbe es eine allmählichere Änderung der Frequenz, die schwieriger zu sehen wäre. Für PM, beachten Sie die deutliche Phasenänderung an den Rändern des gestrichelten Quadratwellen-Nachrichtensignals.
Wie bereits erwähnt, ändert sich, wenn nur die Träger-Sine-Wellen-Amplitude in Bezug auf die Zeit (proportional zum Nachrichtensignal), wie es bei der AM-Modulation der Fall ist, ändert sich der I/Q-Flugzeuggraph nur in Bezug auf die Entfernung vom Ursprung zu den I/Q-Punkten, wie im folgenden Bild gezeigt:
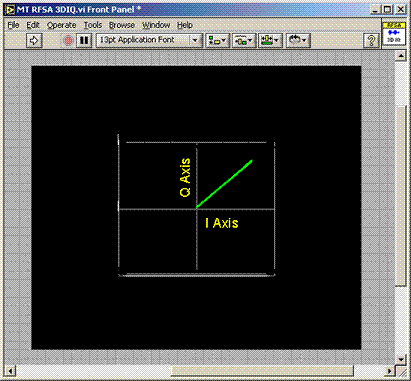
Abbildung 6. I/Q-Daten im Komplex
Die vorige Zahl zeigt, dass die I/Q-Datenpunkte nur in Amplitude variieren, wobei die Phase bei 45 Grad festgelegt ist. Über das Nachrichtensignal kann man nicht viel sagen, nur dass es amplitude moduliert ist. Wenn Sie jedoch beobachten, wie die I/Q-Datenpunkte in Bezug auf die Zeit unterschiedlich sind, können Sie im Wesentlichen eine Darstellung des Nachrichtensignals sehen. Mit der 3D-Grafiksteuerung von LabVIEW können wir die dritte Achse der Zeit zeigen, um das Nachrichtensignal zu veranschaulichen.
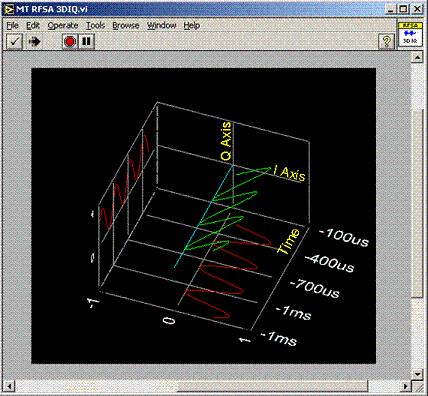
Abbildung 7. Darstellung der Magnitude vs. Zeit
Abbildung 7 zeigt die gleichen Daten wie 2D I vs. Q-Plot in Abbildung 6. Die Größe der Signalspure moduliert in einem sinusförmigen Muster, was darauf hindeutet, dass das Nachrichtensignal eine Sinuswelle ist. Die grüne Spur stellt die Amplituden- und Phasendaten in einem polaren Koordinatensystem dar, während die roten Spuren die Projektionen dieser Wellenform auf die I- und Q-Achsen darstellen, die die einzelnen I- und Q-Wellenformen darstellen.
Wir können die gleiche Art von Beispiel mit PM zeigen, wie in der folgenden Abbildung gezeigt:
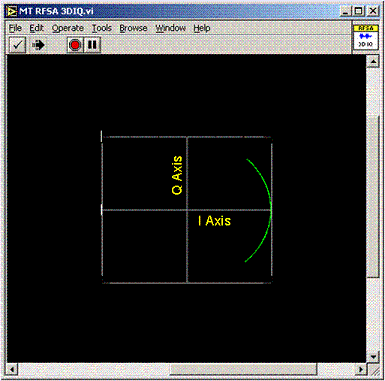
Abbildung 8. Polar Darstellung der Phase vs. Zeit
Sie können sagen, dass das Nachrichtensignal phasenmoduliert ist, da die Amplitude konstant ist, aber die Phase sich ändert (moduliert). Sie können die Form des Nachrichtensignals in Bezug auf die Zeit nicht sehen, aber Sie können sehen, dass die minimalen und maximalen Signalpegel des Nachrichtensignals durch Phasenabweichungen von -45 Grad bzw. +45 Grad dargestellt werden.
Die Zeitachse kann verwendet werden, um dieses Konzept besser zu verstehen, wie in der folgenden Abbildung gezeigt wird:
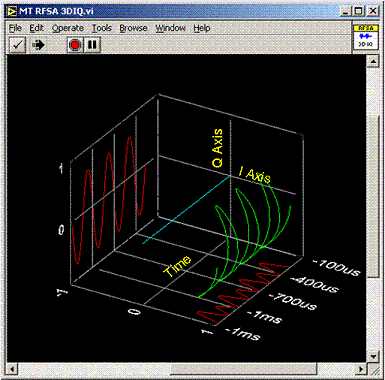
Abbildung 9. 3D Darstellung der Phasenmodulation
Abbildung 9, die im Rahmen des 3D-Diagramms LabVIEW gezeigt wird, zeigt die grüne Spur, die in einer sinusoiden Art und Weise in Bezug auf die Zeit variiert. Die Projektionen auf die I- und Q-Achsen stellen die einzelnen I- und Q-Wellenformen dar, die der PM- Sinuswelle mit fester Größe und oszillierender Phase entsprechen.
Im Wesentlichen stellen die I/Q-Daten das Nachrichtensignal dar. Da die I/Q-Datenwellenformen kartesische Übersetzungen der polaren Amplitude und Phasenwellenformen sind, können Sie Schwierigkeiten haben, die Art des Nachrichtensignals zu bestimmen. Vergleichen Sie zum Beispiel die roten I und Q-Spuren auf dem 3D I vs. Q-Plots in Abbildung 9 bis zur grünen Spur in Abbildung 9. Wenn Sie Amplitude vs. Zeit für die AM sine Welle planen, würden Sie das Nachrichtensignal sehen. Wenn Sie die Phasendaten vs. Zeit für die AM-Sine-Welle plotten, hätten Sie eine gerade Linie. Sie würden auch neun Wellen für die I vs. Zeit- und Q vs. Zeitwellenformen sehen, aber die Skala wäre aus, und dies wäre nicht unbedingt der Fall für komplexere digitale Modulationsschemata, bei denen sowohl Amplitude als auch Phase gleichzeitig moduliert werden.
3. Also warum I/Q-Daten verwenden?
Da Amplitude und Phasendaten intuitiver erscheinen, können Sie davon ausgehen, dass Sie polare Amplituden- und Phasendaten anstelle von kartesischen I- und Q-Daten verwenden sollten. Praktische Hardware-Design-Anliegen machen jedoch I- und Q-Daten zur besseren Wahl.
Die genaue Variation der Phase einer Hochfrequenz-Träger-Sine-Welle in einem Hardware-Schaltkreis nach einem Eingabenachrichtensignal ist schwierig. Ein Hardware-Signalmodulator, der die Amplitude und Phase einer Träger-Sine-Welle manipuliert, wäre daher teuer und schwer zu entwerfen und zu bauen und, wie sich herausstellt, nicht so flexibel wie eine Schaltung, die I- und Q-Wellenformen verwendet. Um zu verstehen, wie man die Phase eines HF-Trägers nicht direkt manipuliert, verweisen Sie auf die folgenden I/Q-Modulationsgleichungen:
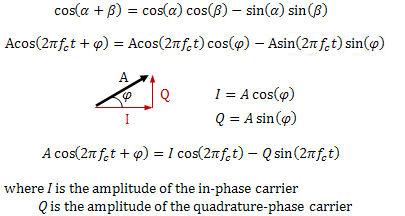
Abbildung 10. Mathematische Hintergrund der I/Q Modulation
Nach der trigonometrischen Identität, die in der ersten Zeile von Abbildung 10 gezeigt wird, multiplizieren Sie beide Seiten der Gleichung durch A und ersetzen Sie 2 .c Dann ersetzen Sie I für A cos() und Q for A sin() um eine Sinuswelle mit der auf Linie 3 angezeigten Gleichung darzustellen.
Denken Sie daran, dass der Unterschied zwischen einer Neun- und einer Cosinenwelle der gleichen Frequenz ein 90-Grad-Phasenversatz zwischen ihnen ist. Im Wesentlichen bedeutet diese Tatsache, dass Sie die Amplitude, Frequenz und Phase einer modulierenden Träger-Sine-Welle steuern können, indem Sie einfach die Amplituden separater I- und Q-Eingangssignale manipulieren. Mit dieser Methode müssen Sie die Phase einer HF-Träger-Sine-Welle nicht direkt variieren. Sie können den gleichen Effekt erzielen, indem Sie die Amplituden der Eingabe-I- und Q-Signale manipulieren. Natürlich ist die zweite Hälfte der Gleichung eine Neun-Welle und die erste Hälfte ist eine Cosin-Welle, so dass Sie ein Gerät in den Hardware-Schaltkreis aufnehmen müssen, um eine 90-Grad-Phasenverschiebung zwischen den Trägersignalen zu induzieren, die für die I- und Q-Mischer verwendet werden, aber diese Ergänzung ist ein einfacheres Designproblem als die oben genannte direkte Phase.
Bild 11 Hardware-Diagramm eines I/Q Modulators
Abbildung 11 zeigt ein Blockdiagramm eines I/Q-Modulators. Die Kreise mit einem "X" stellen Mischer dar - Geräte, die Frequenzvermehrung und entweder Upconvert- oder Downconvert-Signale ausführen (hier umrechnen). Der I/Q-Modulator mischt die I-Wellenform mit der HF-Träger-Sine-Welle und mischt das Q-Signal mit der gleichen HF-Träger-Sine-Welle bei einem 90-Grad-Phasen-Offset. Das Q-Signal wird vom I-Signal (genau wie in der Gleichung in Zeile 3 in Abbildung 10) abgezogen, das die endgültige HF-Modulationswellenform erzeugt. In der Tat ist die 90-Grad-Verschiebung des Trägers die Quelle der Namen für die I und Q-Daten - I bezieht sich auf In-Phase-Daten (weil der Spediteur in der Phase ist) und Q bezieht sich auf Quadraturdaten (weil der Träger um 90 Grad ausgeglichen ist). Diese Technik ist als quadrature upconversion bekannt, und Sie können denselben I/Q-Modulator für jedes Modulationsschema verwenden. Der I/Q-Modulator reagiert lediglich auf Änderungen in I und Q-Waveform-Amplituden, und I- und Q-Daten können jede Veränderung in der Größe und Phase eines Nachrichtensignals darstellen. Die Flexibilität und Einfachheit (bezogen auf andere Optionen) des Designs eines I/Q-Modulators ist der Grund, warum es so weit verbreitet und beliebt ist.
I/Q Daten für Dummies
Dies ist eine Beschreibung der Verwendung von I/Q Data (aka "analysiertes Signal"), die ein Signal darstellt. Da das Thema durchaus verwirrend sein mag, habe ich hier dasselbe aus unterschiedlichen Ansichten beschrieben. Wenn Sie die Informationen etwas überflüssig finden, liegt es daran, dass sie es sind. Unterschiedliche Ansichten mögen verschiedene Leser ansprechen, und wenn etwas unklar erscheint, lesen Sie weiter und es könnte später verständlicher sein - hoffentlich.
Warum I/Q Daten?
I/Q Data ist eine Signaldarstellung, die viel präziser ist als nur die Verwendung einer Reihe von Proben der momentanen Amplitude des Signals. Werfen Sie einen Blick auf das folgende Signal unten.
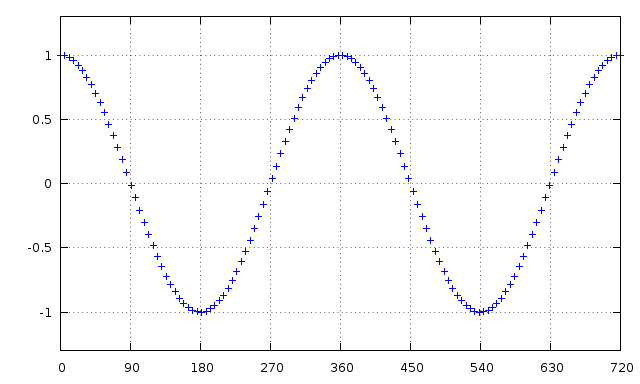
Das ist es, womit Sie möglicherweise arbeiten. Warum also I/Q Data - ist das nicht gut genug?
Nicht wirklich. Wir haben hier ein paar Probleme.
- Erstens ist es unmöglich, die Frequenz dieses Signals zu bestimmen. Sicher, es sieht einfach genug aus, schauen Sie sich nur die Periodenlänge an? Es stimmt, aber Sie haben keine Ahnung, ob es eine positive oder negative Frequenz ist, da sie beide die gleiche Kurve erzeugen. I.e. cos(x) Dies wird zu einem Problem, mit dem Signal zu arbeiten. Mischen (vermehren) zwei Signale und es wird mehrere Lösungen aufgrund der Ungewissheit des Zeichens verursachen: f1 - f2 . f2 . f1 und f1 - f2.
- Zweitens ist es schwer, die Kraft (Peak Amplitude, Hülle) des Signals zu bestimmen. Grundsätzlich kann man hier nur die Spitzenamplitude bei 0°, 180°, 360° usw. sehen, und woher weiß man, dass die Kraft auch überall gleich ist? Und haben Sie das Signal genau auf dem Höhepunkt geschlagen? Sie wissen es wirklich nicht.
I/Q Data löst das. Anstatt das Signal als flache Kurve wie oben zu betrachten, betrachten Sie es als Korkenzieher (helix, Spirale, Spulenfeder) in drei Dimensionen.
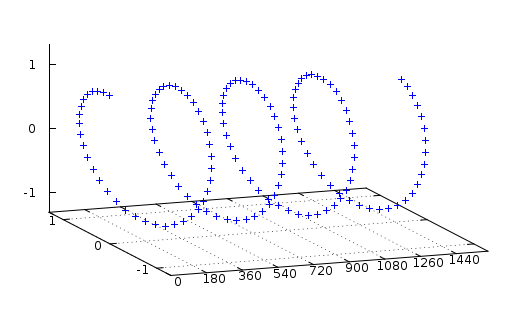
Wenn Sie sich diese Kurve von der Seite ansehen, erhalten Sie tatsächlich die gleiche Grafik wie die erste oben. Ihr "echtes" Signal ist eigentlich diese 2D-Projektion dieses Korkenziehersignals. Das ist Ihr "Ich" in I/Q Daten.
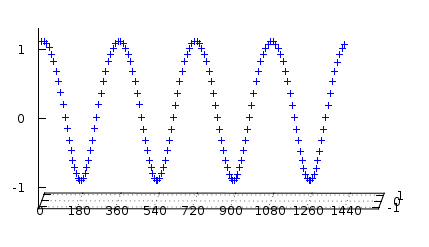
Jetzt schauen Sie sich den Korkenzieher von oben an. Das sieht ziemlich ähnlich aus, aber wie Sie sehen, ist es aus der Phase 90° ab Null, nicht bei einem wie dem anderen. Dies ist der Q-Teil Ihrer I/Q-Daten.
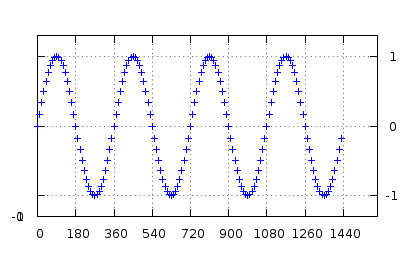
Wenn Sie nun die Korkenzieher entlang der Zeitachse betrachten, werden Sie sehen, wie sie sich gegen den Uhrzeigersinn windet. Das bedeutet, dass wir wissen, dass die Frequenz positiv ist. Es könnte auch im Uhrzeigersinn wunden und immer noch das gleiche I-Signal (Projektion) erzeugen, aber ein anderes Q-Signal, was eine negative Frequenz darstellt.
Sie sehen auch, dass der Radius des Korkenziehers bei jeder Probe konstant ist, wenn in mir groß in Q und umgekehrt. Der Radius ist die Spitzenamplitude Ihres Signals.
Die Achsen sind natürlich 90°, so dass der Radius gleich sein muss (I2+Q2)1/2. Dies ist die Spitzenamplitude Ihres Signals, und wie Sie sehen können, wissen Sie dies für jede Probe.
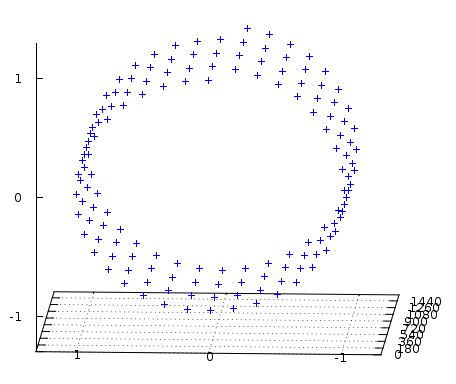
Was ist I/Q Data?
Wie Sie jetzt verstehen, ist die I/Q Data Sample die Koordinaten Ihres Signals, wie man die Zeitachse des Korscrews sieht.
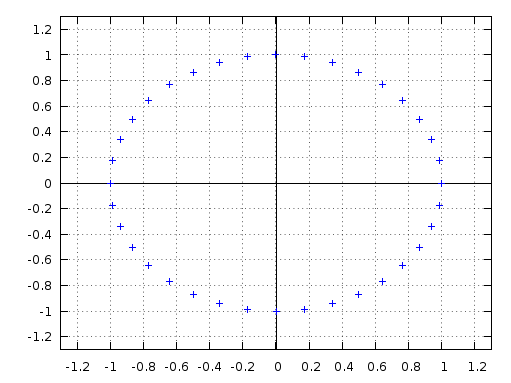
Sie könnten ein Einwände erheben, dass Ihr Signal keine reine Cosinenfunktion ist, wie wir sie hier gezeigt haben, und es könnte sehr wahr sein. Dennoch kann jede einzelne Probe Ihres Signals als solche beschrieben werden, d.h. mit einer Peak-Amplituden-Zeiten von einem Phasenwinkel.
Jeder einzelne Punkt Ihres Signals kann als Funktion A-cos beschrieben werden
Da Sie jede Amplitude A und Winkel frei wählen können - muss dies natürlich wahr sein (solange das Signal kontinuierlich ist). Der Wert von A'cos ist die II-Komponente des I/Q-Signals, d.h. Ihr echtes Signal. Beachten Sie, dass dies nur Ihr Signal in einem einzigen Punkt beschreibt, d.h. eine Probe. Die nächste Probe gibt Ihnen eine neue I und Q, die sehr wahrscheinlich zu einem weiteren Amplituden- und/oder Phasenwinkel führt, der die Modulation des Signals widerspiegelt.
Eine Probe I/Q Daten
Ok, lasst eine Probe von I/Q-Daten nehmen und sehen, was sie darstellt. Dies nennt man auch einen Phasenvektor oder Phasor.
I
Q 0.40
Lassen Sie dies in der komplexen Ebene zeichnen.
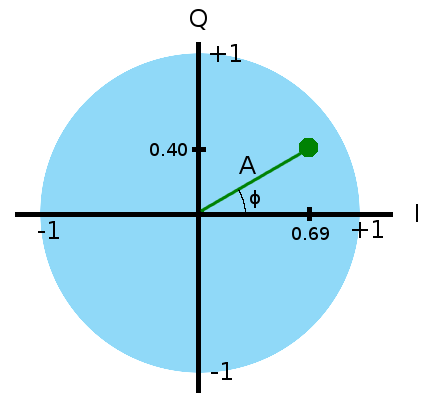
Lassen Sie uns sehen, was uns das über unseren Datenpunkt sagt.
- Die momentane Amplitude unseres realen Signals ist per Definition I. 0.69
- Pythagoras sagt uns, dass die Amplitude A der Cosine-Welle
(0.69²+0.40²)1/2 = 0.8 - Trigonometrie sagt uns, dass unser Winkel +30° in unsere Cosine-Welle ist.
- Halten Sie es, sagen Sie, welche Cosine-Welle?
Nun, I/Q geht tatsächlich davon aus, dass Ihr echtes Signal (ich, das ist) als das Funktion I . A-cos()
Da Sie frei sind, A zu wählen und - das muss natürlich wahr sein, solange die Funktion kontinuierlich ist. Denken Sie daran, dass wir jetzt eine einzelne Probe betrachten, d.h. einen Punkt in der Zeit.
So erhalten wir durch die Verwendung von IQ Data nicht nur die momentanen Werte unseres Signals, sondern auch die Funktion, die es erzeugt. Wenn wir oben zusammenmachen, bekommen wir:
Das eigentliche Signal I - 0.8cos (30°)
- I/Q Data ist die Darstellung (Datentyp) dieser Cosinenfunktion.
I/Q Data ist die rechteckige Darstellung der Polarnotation, die wir oben verwendet haben. Es gibt eine einzigartige Transformation zwischen den beiden, und die verschiedenen Notationen haben unterschiedliche Eigenschaften, die mit ihnen berechnen. Die rechteckige Form von I/Q-Daten wird aufgrund der einfachen Hardware-Implementierung der häufigsten Operationen gewählt.
I/Q-Daten bestehen aus I und Q, die als zwei separate Variablen dargestellt sind, ein Vektor der Länge zwei, oder öfter, die komplexe Zahl I + Q i (y, I ist der reale Teil).
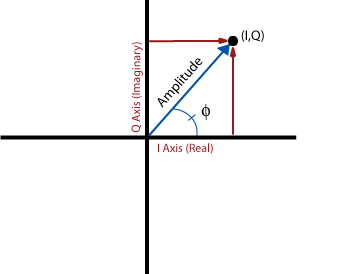
Beachten Sie, dass die Amplitude oben die Wellenspitzen-Amplitude ist, nicht die momentane Amplitude.
- Ich bin die aktuelle momentane Amplitude des Signals (d.h. das Reale Signal)
Für eine einfache Funktion wie sine ist die Phasenverschiebung das, was das Signal früher war, aber für ein Signal mit mehr als einem Neun-Komponenten reflektiert Q eine -90°-Schicht der einzelnen Komponenten und nicht das Verbundsignal als solches. Um ein echtes Signal in ein I/Q-Datensignal umzuwandeln, ist eine diskrete Fourier-Transformation erforderlich (Hilberts transform).
Verschiedene Möglichkeiten, die gleiche I/Q Data Sample darzustellen
Es gibt mindestens drei gemeinsame Wege, um die I/Q-Datenprobe darzustellen. Unterschiedliche Darstellungen gibt Ihnen verschiedene Vor- und Nachteile. Einige sind leichter hinzuzufügen, andere sind leichter zu vermehren usw. Dies kann bei der Implementierung wichtig sein, was zu weniger komplexer Hardware/Software mit der besten Darstellung führt.
Die rechteckige Form
Die I/Q-Daten auf dem Formular Q und I werden "rechteckig" (oder "Cartesian") Form genannt, da sie als Positionen in einem Koordinatensystem angesehen werden können. I und Q sind die x- und y-Achse. Dies ist die häufigste Darstellung, die Sie gewohnt sind. Diese Form ist am häufigsten aufgrund der einfachen Modulierung/demodulieren in der Hardware. Mehr dazu später.
- Als komplexe Zahl: I + Q i
Die Polarform
- Amplitude und Winkel
I - Amplitude-cos (Winkel)
Q - Amplitudensin (Winkel)
Die Amplitude ist die Spitzenamplitude der Cos (und Sünde) Funktion, und der Winkel ist, wie weit in der Periode von Null bis 360° Sie sind (oder 0 bis 2, wenn Sie Radians bevorzugen).
Euler Form
Seit cos() + i sin() . e i .
Ae i
Dies könnte (nicht?) die intuitivste Darstellung der Probe sein. - dreht den Winkel, wie man sie in der polaren Darstellung sieht, und A ist natürlich die Amplitude. Wenn man dies erkennt, wird die Eulers-Identität offensichtlich. Denn - ist die Drehung des Vektors in der komplexen Ebene, die es eine halbe Kurve, 180° oder - Radians dreht, führt zu einem realen Teil von -1 und kein imaginärer Teil, daher:
e .i +1 - 0
"Der Student sollte dies sofort klar finden,
sonst wird er nie ein Mathematiker der ersten Rate sein"
-- Carl Friedrich Gauß
Positive versus negative Frequenz
Es ist jetzt leicht zu sehen, dass wir mit I/Q die Signalfrequenz entweder als positiv oder negativ darstellen können. Werfen Sie einen Blick auf die beiden I/Q Signale rot und blau unten nach links und vergleichen Sie sie mit ihren entsprechenden realen Projektionen. Es ist so offensichtlich, dass sie sich in den Zeichen in I/Q unterscheiden, da es unmöglich ist, die Zeichen nur mit der realen Signalkomponente zu bestimmen (weder die I noch die Q-Projektion getrennt).
(Aside: Ich habe sie im Vergleich zueinander etwas aus der Phase herausgebracht, da sie sonst überhaupt nicht in der realen Darstellung rechts unterscheiden können. Bitte beachten Sie auch, dass ich hier bin, ruhig unkonventionell, mit der x-Achse im Phasor für das imaginäre Q)
Das gleiche Signal (naja, mehr oder weniger) in einer 3D-Darstellung.
Die II-Komponenten (Sengansicht):
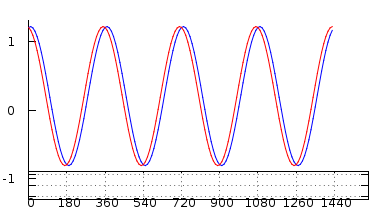
Die QQ-Komponenten (Top-Ansicht):
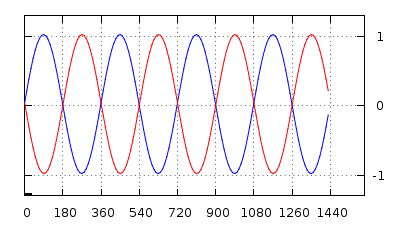
Die I/Q Signale in 3D:
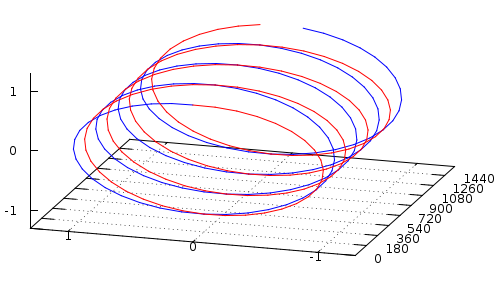
Wie der Nyquist-Shannon-Sampling-Verkostungssatzes besagt, dass man nur Frequenz bis f/2mit einer Stichprobenrate von f. Das ist immer noch wahr Verwendung von IQ-Daten, aber da Sie jetzt negative Frequenzen darstellen können das Signalspannen [-f/2..+f/2]im Vergleich zu [0..+f/2]mit einem Real-Signal Daher wird der Bereich in der Tat verdoppelt. Verwenden eines Stichproben von fund Sie können jetzt eine Signalspanne von fauch. Zwei zum Preis!
Mischen und Multiplizieren von Signalen
Die Verwendung realer Signale oder IQ-Signale liefert unterschiedliche Ergebnisse, wenn Sie sie multiplizieren. Denn nur mit der realen Komponente ist es nicht möglich, den Phasenwinkel des Signals eindeutig zu bestimmen, daher unmöglich, eine positive Frequenz von einem Negativ zu unterscheiden.
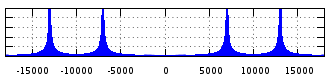
Multiplizieren von zwei Signalen f1 und f2 in der realen Domäne:
F1 - F2 - F2 (-)f1
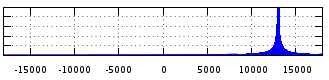
Mit IQ-Daten werden jetzt die Zeichen gegeben, und das Ergebnis ist eindeutig:
f1 f2
Ein Frequenzspektrum in der realen Domäne zeigt normalerweise nie die negative Seite, da es aufgrund der Unsicherheit des Zeichens der Frequenz des realen Signals immer symmetrisch um Null sein muss - daher die Klammern um das Zeichen von f1in der ersten Formel, die die realen Signale mischt. Ich habe hier die negative Seite für illustrative Zwecke aufgenommen, trotz ihrer Entlassung.
Zwei komplexe Zahlen zu multiplizieren, ist in der polaren Darstellung am einfachsten zu verstehen. Die Amplitude wird vervielfacht und der Winkel addiert.
A 1 . i. 1 .A 2 2. 2 - A 1 A 2 e i (- 1 1+ 22
Die Erkenntnis, dass der Winkel unter Multiplikation hinzugefügt wird, macht es offensichtlich, dass die Frequenzen hinzugefügt werden.
Und mit der Zeit ...
Schauen wir uns das in der Zeitdomäne an. Um es einfacher (setzlich!) zu machen, die DFT in unseren Köpfen zu berechnen, wählen wir wirklich einfache Zahlen. Lass uns mischen fmit -f. Mit I/Q wäre das Ergebnis null, nicht mit I/Q, es wäre Null und 2f(und -2f, aber in real ist es kein Unterschied). Nun, 2f, da die Null (DC) Komponente ... Null ist, d.h. nicht da. Ich habe Ihnen gesagt, dass wir einfache Zahlen verwenden würden. :-)
Hier haben wir fund -fals blau und rot. Grün ist das Produkt der komplexen Signale, und schwarz ist das Produkt der entsprechenden realen Signale.
Rechts. Grün ist ganz richtig Null in der Frequenz, und das reale (R) Signal schwarz ist sehr klar 2f(die DC-Komponente verschwindet ganz natürlich in der realen Welt).
Bitte über die Tatsache, dass der grüne Mix der I/Q-Signale immer noch die volle Amplitude hat, obwohl die Frequenz Null ist. Dies ist durchaus möglich, eine DC-Komponente in I/Q so darzustellen, wo die schwarze DC-Komponente mit echtem Stück einfach verschwindet. Keine Sorge, dass der grüne Mix nicht perfekt auf die Achse ausgerichtet ist, nur weil blaue und rote I/Q-Signale etwas außerhalb der Phase sind.
(und ja, ich benutze die Y-Achse für das echte Signal hier)
Ein komplexeres Beispiel
Wenn wir jetzt die gleichen Signale wie in der Frequenz-Domäne oben betrachten, erhalten wir das Mischen von 10 kHz (rot) mit 3 kHz (blau) und das Ergebnis mit I/Q (grün) oder mit realem (schwarz) wie unten gesehen.
Bemerkenswert ist hier, dass der I/Q-Mix (grün) eine reine Neunwelle höherer Frequenz ist, aber der echte Mix (schwarz) ist eindeutig ein Verbund aus mehreren Frequenzen (10-3, 10+3), genau wie im Frequenzspektrum oben.
RF Down Konvertieren zu I/Q Daten
Es gibt einen fundamentalen Unterschied zwischen einem Basisband und einem modulierten HF-Signal. Das modulierte Signal fährt auf einem Träger einer bestimmten Frequenz, aber das Basisbandsignal hat keine feste Frequenz. Aus diesem Grund haben wir die Möglichkeit, das zweidimensionale I/Q-Signal auf das eindimensionale HF-Signal zu kodieren, ohne etwas zu verlieren. Magie!
Der Träger einer bestimmten Frequenz hat zwei Parameter, die wir ändern können, seine Amplitude und Phase. Das ist es, was wir verwenden, um unsere I/Q-Daten zu kodieren. Wir können es auf dem Träger der Frequenz f kodieren (t für die Zeit):
Moduliertes Carrier RF - Icos(2-ft) + Qsin(2-ft)
Durch das Hinzufügen eines Cosin mit seiner entsprechenden Neunkomponente der gleichen Frequenz (d.h. dem Träger) ändern wir die Phase und Amplitude des resultierenden HF-Signals. Es zurück zu verwandeln ist so einfach.
I - Tiefpass (RF-cos(2-ft))
Q - Tiefpass (RF-Sin(2-ft))
Haben Sie es? Der Träger hat eine vordefinierte Frequenz, daher eine feste Phase als Referenz. Das Grundband nicht, daher die Notwendigkeit, die Phase mit zwei Parametern explizit darzustellen.
Noch selbst wenn dies auf dem Papier in Ordnung aussieht, kann die Phase in Wirklichkeit aufgrund der Tatsache driften, dass die Sender und Empfänger Oszillatoren nie perfekt synchron sind, aber sich sowohl in Phase als auch in der Frequenz ein wenig unterscheiden. Dafür können die Absender I und Q im Vergleich zu den Empfängern I und Q aus der Phase heraus sein, aber der relative Winkel von I und Q ist immer korrekt genug, sowie die Amplitude.
Negative Frequenzen kein Problem auch nicht. Da der Träger viel höher ist als die Modulation, erzeugt eine negative Signalfrequenz immer noch eine positive Trägerfrequenz. Es ist das erste Mal, wenn Sie Basisband vom Träger entfernen, müssen Sie eine Möglichkeit haben, es wieder negativ darzustellen, d.h. mit I/Q-Daten.
Formeln
Einige Formeln, die mit I/Q-Signalen berechnen, die zwischen polarer und rechteckiger Form usw. übersetzen.
Peak Amplitude A (I2+Q2)1⁄2
Phase-Knirnwinkel - tan-1(Q/I)
I.
Q - A-sin()
IQ-Daten in ein klares Signal umzuwandeln: Ich bin das Originalsignal.
Euler Form: A. i . . A. (cos() + i-sin())
Einige Beispiele
Die folgenden Beispiele mögen ziemlich hübsch aussehen, aber interpretieren sie mit einem Körnchen Salz. Das modulierte Trägersignal wird nicht mit I/Q-Daten dargestellt. Mehr darüber, wie man das I/Q-Datensignal vom nicht---Q-Datenmodulmodulator später ablenügt, sobald ich eine pädagogische Erklärung herausgefunden habe. :-)
AM-Modulation im IQ
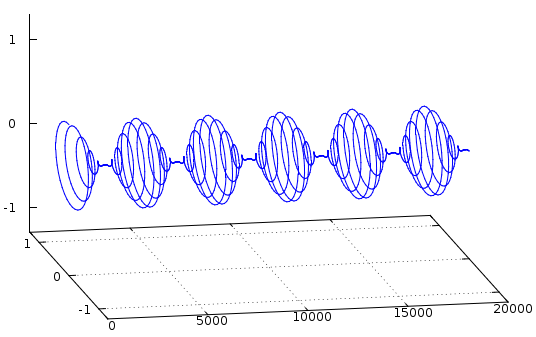
Derselbe Graph von der Seite gesehen, d.h. nur als ich.
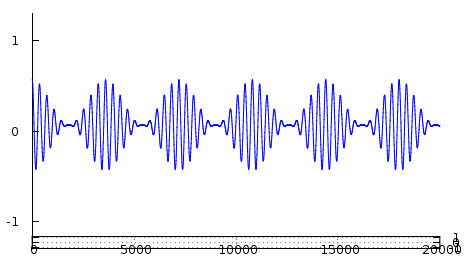
Die Amplitude wird als (I2+Q2)1⁄2 für jede Probe angegeben, d.h. auch für Proben mit dem realen Bauteil I gleich Null.
FM-Modulation im IQ
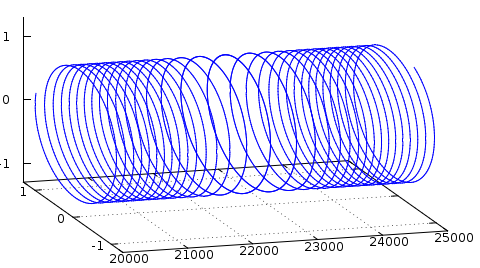
Beachten Sie, dass die Amplitude konstant ist.
Derselbe Graph, wie von der Seite gesehen, d.h. als nur.
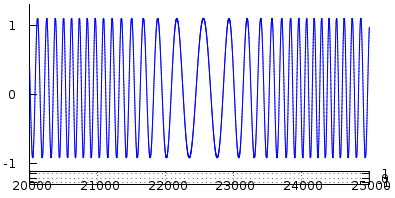
Ein wenig Trick
Werfen Sie einen Blick auf das folgende Signal in I (real) nur.
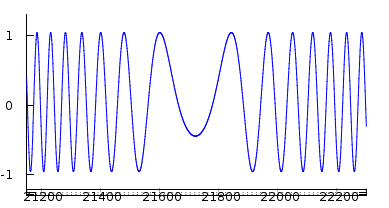
Drei Teile links, Mitte und rechts. Die Frequenz nach links ist ungefähr gleich wie die Frequenz rechts? Ja, wenn man nur ich hat, kann man den Unterschied nicht erkennen. Aber schauen Sie sich nun das gleiche Signal in I/Q an.
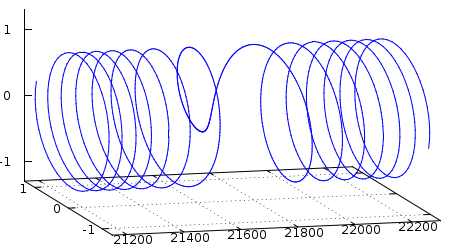
Sie sehen hier, dass das Signal seine Richtung in der Mitte ändert, d.h. von einer positiven Frequenz zu einem Negativen. Um dies zu erkennen, müssen Sie I/Q verwenden. Der eigentliche Teil, den ich allein bin, ist nicht genug. Deshalb ist ein Signal in der realen Domäne (nur ich) immer symmetrisch um Null in der Frequenzdomäne. Bei I/Q-Signalen ist das nicht der Fall.
I/Q - nur eine mathematische Konstruktion?
Manchmal bekomme ich den Einwand: "Ich/Q-Daten sind schön, aber es ist nur eine mathematische Konstruktion. Das wahre Signal ist real".
Ich bin damit nicht einverstanden. Ich würde sagen, das wahre Signal ist komplex, und das wirkliche Signal ist eine unvollständige Projektion davon. Das wahre Signal hat tatsächlich die Attribute Phase und Amplitude für jede Probe (d.h. Punkt in der Zeit). Daher ist das wahre Signal nicht nur komplex, sondern dreidimensional: Phase, Amplitude und Zeit.
Schauen Sie zum Beispiel beim Pendel. Seine Schwingungen können als Signal beschrieben werden. Die Energie des Pendels oszilliert zwischen potentieller Energie und kinetischer Energie. Um den Zustand des Pendels zu repräsentieren, müssen Sie sowohl seine kinetische Energie als auch mögliche Energie angeben. Die kinetische wie auch die potentielle Energie sind sowohl sehr reale (in beiden Aspekten) physischen Eigenschaften des Pendelzustands. Wenn man einen auslässt, weiß man wirklich überhaupt nichts über den Zustand des Pendels. Um die Energie des Pendels abzuschätzen, müssten Sie eine Reihe von Proben nehmen, um das Maximum herauszufinden, genau so, wie Sie die Amplitude eines Signals in real usw. herausfinden würden. Und denken Sie daran, wenn das Signal moduliert ist, d.h. nicht statisch, garantiert nichts, dass die Amplitude in Ihrer Probenserie konstant bleibt.
Das obige Beispiel ist nicht analog zu I/Q-Daten - dieses Beispiel sind I/Q-Daten. Nutzung Ifür kinetische Energie Qfür potentielle Energie, und da bist du.
Für die elektromagnetische Welle würde ich sagen, dass die Parallele zum Pendel die Übertragung von Energie zwischen den elektrischen (E) und magnetischen (B) Feldern ist. Sicher, sie sind in der Phase und nicht um 90° verschoben, aber denken Sie daran, dass die Energie eines Magnetfeldes proportional zu seiner Veränderungsrate (Derivat) ist, und das E-Feld wird um 90° in den Derivate B verschoben, was die Energiesumme im Laufe der Zeit konstant macht.
Nutzungsbedingungen
Iist die In-Phase-SignalkomponenteQist die Quadrature Signalkomponenteiist die mathematische Konstanteiwiei² = -1Awird für die Spitzenamplitude, die Hülle, des Signals verwendetϕ(phi) ist der Phasenwinkeleist die Basis für den natürlichen Logarithm⊗ist die Betriebsmischfrequenz⋅ist die Operation Multiplikation- "real" wird im Gegensatz zu I/Q verwendet, und nicht notwendig die I-Komponente, sondern "real" wie in "nicht komplex" oder "real".
- R bezeichnet Real Zahlen.
- "Real" bezeichnet das nicht imaginäre Signal oder die Komponente, um sich von "real" wie im "wahren" Signal zu unterscheiden.
- C bezeichnet komplexe Zahlen.
DCfür "Direktstrom", die Frequenz Null.- "Projektion" ist die Reduktion von Abmessungen in gleicher Weise, wie eine Kamera ein 3D-Objekt in ein 2D-Bild projiziert.
Praxis ist vertreten Iwie xAchse und Qwie yAchse in 2D-Diagrammen und Ials realer Teil und Qals imaginärer Teil einer komplexen Zahl. Ich weiche oft davon ab, um die Illustrationen leichter lesbar zu machen. Es ist keine Bedeutung, wenn Sie Iund Q, die Bedeutung ist, dass sie orthogonal (90°) zueinander sind, und die Verwendung einer komplexen Darstellung ist auch nur Bequemlichkeit, daher keine Bedeutung, wenn Qist "up" in einem Graphen, I"up" im nächsten, oder welche Sie zufällig als realen jeweils imaginären Teil in der komplexen Zahl darstellen, wenn Sie überhaupt eine komplexe Darstellung verwenden.