Passives Radar mit Software-Defined Radio zur Detektion von Flugzeugen.
Zusammenfassung
Passives Radar mit Software-Defined Radio zur Detektion von Flugzeugen.
Passives Radar bietet mehrere Vorteile gegenüber allgegenwärtigen aktiven Systemen. Dazu gehören geringe Systemkosten und geringe Energieanforderungen.
Diese Eigenschaften machen es möglich, passive Radarsysteme weitflächig in entlegenen Gebieten für Anwendungen wie nationale Grenzsicherheit einzusetzen. Software-Defined Radio ermöglicht es, flexible passive Radarsysteme schnell in Software mit minimalem Hardwareaufwand umzusetzen. Das Ziel dieser Forschung ist es, ein passives Radarsystem mit Software-Defined Radio zu implementieren und seine Leistung zu bewerten. Diese Arbeit beschreibt die Umsetzung eines solchen Systems und präsentiert eine Analyse der mit dem System gesammelten Daten.
1. Einleitung
Diese Arbeit beschreibt die Implementierung eines passiven Radars unter Verwendung des Universal Software Radio Peripheral (USRP) und GNU Radio. Passives Radar nutzt Umgebungsfunksignale zur Erkennung und Entfernung von Flugzeugen. Die Umsetzung von passivem Radar mithilfe von softwaredefinierten Radios (SDR) ist durch die Verfügbarkeit leistungsstarker Computer, kostengünstiger SDR-Hardware und Open-Source-Software zur Unterstützung praktikabel geworden. Die Ergebnisse werden für kleine, niedrig fliegende Flugzeuge präsentiert.
Ein ähnliches System wie das hier vorgestellte konnte Flugzeuge in einer Entfernung von etwa 100 km erkennen [1]. Wie beim hier präsentierten System wurde die Signalverarbeitung in [1] zwischen Hardware und Software aufgeteilt. Ein Großteil der von dem System in [1] verwendeten Hardware wurde nicht von Software gesteuert. Das in dieser Forschung implementierte System verlagert einen Großteil der Signalverarbeitungsverantwortung von Hardware auf Software. Das System in [1] verwendet Hardware, um unerwünschte Signale zu unterdrücken, während das hier vorgestellte System unerwünschte Signale in der Software entfernt. Ein Nachteil der stärker auf Hardware basierten Herangehensweise in [1] ist, dass Hardwareparameter manuell von einem menschlichen Bediener angepasst werden müssen. Zu den manuell anzupassenden Parametern gehören Phasenverschiebung, die Frequenz, auf die der Empfänger abgestimmt ist, und Verstärkung.
Das hier präsentierte System automatisiert diese Prozesse, indem es sie in der Software implementiert. Der Empfänger wird von Software gesteuert, was es ermöglicht, ihn mit Softwareanweisungen abzustimmen. Die Phasenbeziehungen zwischen empfangenen Signalen können automatisch und kontinuierlich von Software mithilfe einer Phasenregelschleife angepasst werden. Die Verstärkung kann statisch in der Software durch Verstärkung oder Abschwächung eines Signals um einen konstanten Faktor oder dynamisch mithilfe einer automatischen Verstärkungsregelung angepasst werden.
Ein weiterer Unterschied des hier präsentierten Systems ist die Verwendung eines digitalen Fernsehsignals anstelle eines frequenzmodulierten Radiosenders. Eine digitale Fernsehstation kann eine höhere Reichweitenauflösung bieten, da sie über eine viel größere Bandbreite verfügt als ein frequenzmodulierter Radiosender.
Hintergrund
Passives Radar unterscheidet sich von dem häufiger verwendeten aktiven Radar dadurch, dass passives Radar nur Echos von Gelegenheitssendern verwendet, anstatt sein eigenes Signal zu senden [2]. Obwohl passive Radarsysteme nicht häufig sind, ist das Konzept nicht neu. Robert Watson-Watt führte 1935 das Daventry-Experiment durch, das vielleicht die erste Anwendung von passivem Radar war [3]. Während des Daventry-Experiments verfolgte Watson-Watt einen Bomber mithilfe einer Kurzwellen-Radiostation.
Wie im Fall von Watson-Watts System sind passive Radarsysteme in der Regel bistatisch, was bedeutet, dass der Empfänger weit vom Sender entfernt ist. Dies unterscheidet sich von aktiven monostatischen Radarsystemen, die Signale am selben Ort senden und empfangen [4]. Nach Definition ist der Sender eines passiven Radarsystems nicht vom Betreiber des passiven Systems gesteuert und wird oft als unkooperativer Illuminator oder Gelegenheits-Illuminator bezeichnet [5].
Bistatische passive Radarsysteme bieten mehrere Vorteile gegenüber aktiven monostatischen Radarsystemen. Die Notwendigkeit, einen teuren Sender zu betreiben, der eine große Stromquelle benötigt, wird durch die Gelegenheitsnutzung eines entfernten Senders beseitigt. Da Tarnflugzeuge darauf ausgelegt sind, sich gegen monostatische Radarsysteme zu verteidigen, kann ein bistatisches Radar sie erfassen [6]. Außerdem könnte ein passives Radarsystem, das mit SDR implementiert ist, die Möglichkeit haben, nach Belieben zwischen mehreren Sendern zu wechseln.
Solche Systeme könnten in großer Anzahl in abgelegenen Gebieten zur Grenzsicherung eingesetzt werden. Der geringe Energiebedarf könnte es ermöglichen, dass die Systeme solarbetrieben sind und somit keine Notwendigkeit besteht, sie in der Nähe von Stromleitungen zu platzieren. Die Systeme könnten als Teile von Sensornetzwerken dienen, wobei die SDRs auch die Kommunikation zwischen den Systemen bereitstellen.
A. Ausdruck von Leistung und Gewinn in Dezibel
Leistung und Gewinn werden oft in Dezibel ausgedrückt, um ihren großen Wertebereich zu komprimieren, der häufig mehrere Größenordnungen umfasst. Ein Wert wird in Dezibel umgerechnet, indem man den dekadischen Logarithmus nimmt und mit 10 multipliziert.
![]() (1)
(1)
Dezibel werden oft verwendet, um die Größenordnungen von zwei Werten zu vergleichen.
![]() (2)
(2)
Um die absolute Leistung auszudrücken, werden Dezibel unter Verwendung einer spezifischen Referenzleistung berechnet. In (1) wird der Referenzwert darauf hingewiesen, dass es sich um eine einzelne Einheit derselben Einheiten handelt, in denen P ausgedrückt wird. Eine häufige Referenzleistung beträgt 1 mW, und die resultierenden Dezibelberechnungen haben die Einheiten dBm.
![]() (3)
(3)
B. Antennendirektivität und Gewinn
Die Menge an Leistung, die von einer Antenne abgestrahlt wird, variiert mit dem Azimutwinkel θ und dem Elevationswinkel φ. Die Strahlungsintensität U(θ, φ) ist die Leistung pro Einheit des festen Winkels, die in eine bestimmte Richtung abgestrahlt wird. Die Gesamtleistung, die von einer Antenne abgestrahlt wird, ergibt sich durch Integration der Strahlungsintensität für alle Richtungen [7].
![]() (4)
(4)
Die durchschnittliche Strahlungsintensität wird durch die Gleichung gegeben.
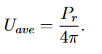 (5)
(5)
Die Richtwirkung gibt die Strahlungsintensität in eine bestimmte Richtung im Verhältnis zur durchschnittlichen Strahlungsintensität der Antenne an. Die Richtwirkung ist definiert durch Gleichung
![]() (6)
(6)
Die Direktivität wird durch den maximalen Wert der Richtwirkung gegeben, der an der Stelle auftritt, an der die Strahlungsintensität am größten ist, nämlich Umax
![]() (7)
(7)
Die Leistungsverstärkung einer Antenne, oder einfach die Verstärkung G, ist ein Maß für die Leistung, die sie in eine bestimmte Richtung im Vergleich zur Leistung abstrahlt, die von einem isotropen Strahler in derselben Richtung abgestrahlt wird, wenn beiden Antennen die gleiche Leistung Pin zugeführt wird. Ein isotroper Strahler ist eine theoretische Quelle, die, wenn sie im Zentrum einer Kugel platziert wird, die Oberfläche der Kugel gleichmäßig beleuchten würde. Die Verstärkung hängt von der Effizienz und der Direktivität der Antenne ab und variiert daher mit azimutalen und elevationswinkeln
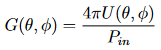 (8)
(8)
Oft werden Antennen mit einem einzigen Verstärkungswert spezifiziert, der tatsächlich die Verstärkung der Antenne in Richtung der größten Richtwirkungsverstärkung ist
![]() (9)
(9)
Die Verstärkung wird in der Regel in Dezibel ausgedrückt
![]() (10)
(10)
Die Gewinnung einer Antenne ist für ausgestrahlte und einfallende Energie identisch [7]. Der Antennengewinn kann grafisch durch ein Strahlungsmuster dargestellt werden, wie in Abbildung 1 gezeigt.
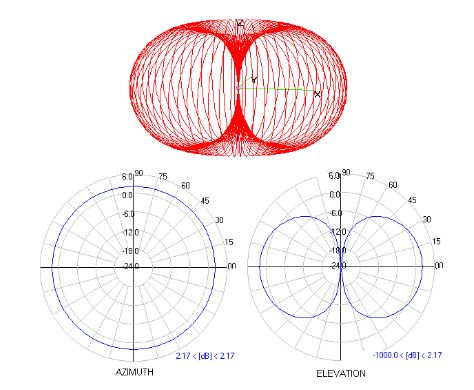
Abb. 1. Strahlungsmuster für eine gängige omnidirektionale Antenne [8]. Das Strahlungsmuster für eine Dipolantenne wird als dreidimensionale Darstellung und als zweidimensionale Azimut- und Elevationprojektionen gezeigt. Die radialen Linien in den zweidimensionalen Mustern sind in Grad markiert, und die Kreise sind in Dezibel im Verhältnis zu einem isotropen Strahler markiert.
C. Radarquerschnitt
Der Radarquerschnitt eines Objekts beschreibt, wie viel Energie es zu einem Radarempfänger reflektiert. Der Radarquerschnitt ist eine imaginäre Fläche, die angenommen wird, um einfallende Strahlung abzufangen. Die Fläche entspricht dem, was notwendig ist, um die Menge an Energie zu erfassen, die, wenn isotrop ausgestrahlt, zu dem Beitrag des Objekts zur Energiedichte am Empfänger führen würde [9]. Die Einheiten des Radarquerschnitts sind Quadrat-Einheiten der Länge, wie bei jeder Fläche. Radarquerschnittsmessungen werden oft in Dezibel relativ zu einem Quadratmeter angegeben. Der Radarquerschnitt eines Flugzeugs variiert erheblich, abhängig von dem Beobachtungswinkel, wie in der Radarquerschnittsdiagramm in Abb. 2 gezeigt.
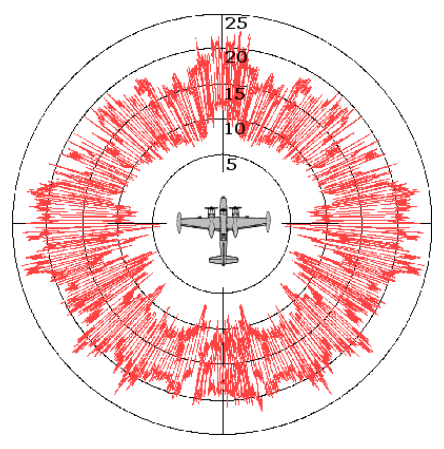
Abb. 2. Typisches Diagramm der monostatischen Radarquerschnittsfläche [10]. Das Diagramm zeigt einen azimuthalen Querschnitt des Radarquerschnitts in der Ebene der Flügel des Flugzeugs. Wie aus dem Diagramm ersichtlich ist, variiert der Radarquerschnitt erheblich mit dem Beobachtungswinkel.
D. Die Radargleichung
Die Radarentfernungs-Gleichung wird verwendet, um die empfangene Leistung aus Echos vorherzusagen. Diese Berechnung kann verwendet werden, um festzustellen, ob ein passives Radarsystem empfindlich genug ist, um gewünschte Ziele in einer gegebenen Umgebung zu erfassen. Die bistatische Radarentfernungs-Gleichung ist definiert durch [11].
![]() (11)
(11)
where
Pr = received signal power
Pt = transmit power
Gt = transmit antenna gain
r1 = transmitter-to-target range
σb = target bistatic radar cross-section
r2 = target-to-receiver range
Gr = receive antenna gain
λ = radar wavelength
Signal-Rausch-Verhältnis
Das Signal-Rausch-Verhältnis kann berechnet werden, indem man (11) durch die Rauschleistung teilt, die durch gegeben ist.
![]() (12)
(12)
where
k = Boltzmann’s constant (1.3806504×10−23 J/K)
T0 = 290 K
B = receiver bandwidth
F = receiver noise factor
Der Störfaktor, F, ist ein Maß für die Verschlechterung des Signal-Rausch-Verhältnisses (SNR), die durch ein Gerät verursacht wird, durch das ein Signal verläuft. Der Störfaktor wird definiert durch
![]() (13)
(13)
Das Signal-Rausch-Verhältnis wird daher durch folgende Formel beschrieben:
![]() (14)
(14)
E. Empfängerempfindlichkeit
Die Empfindlichkeit eines Systems ist ein Maß dafür, wie klein ein Eingangssignal sein kann und dennoch ein nützliches Ausgangssignal erzeugt. Für die Zwecke dieser Forschung wird die minimal nachweisbare Signalstärke oder der Rauschpegel verwendet, um vorherzusagen, ob das System in der Lage ist, eine vom Gleichung (11) vorhergesagte Lecholeistung zu nutzen. Das theoretische minimale nachweisbare Signal kann berechnet werden, indem man die Rauschzahl (NF) des Empfängers addiert, die einfach der Rauschfaktor in Dezibel ausgedrückt ist, zum thermischen Rauschen. Der Rauschfaktor wird durch
![]() (15)
(15)
Gleichung (16) wird in Dezibel ausgedrückt, wie in Gleichung (12). Die mit Gleichung (16) berechnete Leistung ist in Einheiten von dBm angegeben, weshalb das thermische Rauschen mit 1.000 multipliziert wird, um Watt in Milliwatt umzuwandeln. Gleichung (16) ist nützlich, da die Rauschzahl eines Empfängers oft vom Hersteller angegeben wird.
![]() (16)
(16)
F. Der Doppler-Effekt
Der Doppler-Effekt ist die Veränderung der beobachteten Frequenz, die auftritt, wenn sich eine Signalquelle relativ zu einem Beobachter bewegt. Die Verschiebung ist direkt proportional zur Geschwindigkeit und zur Frequenz des Signals. Die beobachtete Frequenzverschiebung wird durch [6] angegeben.
![]() (17)
(17)
where
fd = Doppler frequency shift
v = velocity
c = speed of light
fc = carrier frequency
α = angle between direction of v and line connecting target
and receiving antenna
G. Spektrogramme
Ein Spektrogramm ist eine dreidimensionale Darstellung, die den spektralen Inhalt
eines Signals über einen bestimmten Zeitraum zeigt. Die Magnitude der kurzzeitigen Fourier-Transformation (STFT)
wird über der Zeit-Frequenz-Ebene dargestellt. Die STFT einer Funktion, f (t), ist definiert
als [12]
![]() (18)
(18)
Die STFT (Kurzzeitspektralanalyse) wird einfach durch die Fourier-Transformation über kurze Zeitintervalle, die durch eine Fensterfunktion ausgewählt sind, durchgeführt. Spektrogramme werden in der Regel als Intensitätsbilder dargestellt, wobei die Intensität die Größe der STFT repräsentiert. Jede Zeile des Diagramms repräsentiert das Spektrum des Signals über ein kurzes Zeitintervall. Ein Beispiel für ein Spektrogramm, das das Spektrum eines Audiosignals darstellt, ist in Abbildung 3 zu sehen.
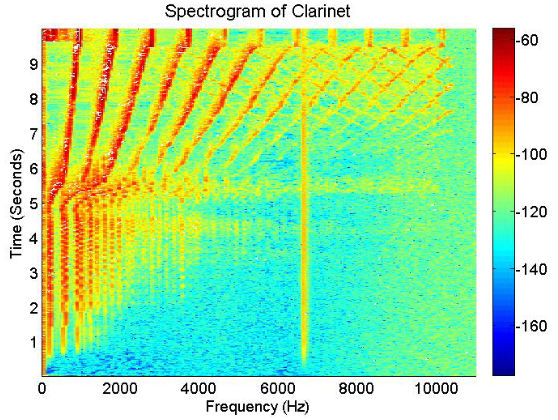
Abb. 3. Beispiel für ein Spektrogramm. Das Spektrogramm einer Klarinette, die die ersten 10 Sekunden von "Rhapsody in Blue" spielt. Mehrere Harmonische, die vom Instrument erzeugt werden, können durch die Betrachtung des Spektrogramms festgestellt werden. Die Tonhöhe beginnt sich etwa bei 5 Sekunden zu erhöhen.
H. Die Kreuz-Ambiguitätsfunktion
Die Kreuz-Ambiguitätsfunktion gibt die Antwort eines Filters wieder, das auf eine bestimmte Dopplerverschiebung und Zeitverzögerung im Verhältnis zu einem Referenzsignal abgestimmt ist [13]. Durch Abstimmen des Filters auf eine bestimmte Dopplerfrequenz und Zeitverzögerung kann das Vorhandensein eines Ziels mit einer bestimmten Geschwindigkeit und an einer spezifischen bistatischen Entfernung festgestellt werden.
Die Kreuz-Ambiguitätsfunktion ist definiert durch [1].
![]() (19)
(19)
where
u(t) = target channel signal
v(t) = reference channel signal
τ = time delay
f = Doppler frequency shift
Die Kreuzambiguitätsfunktion hat eine wichtige Eigenschaft für die Zwecke dieser Arbeit.
Eigenschaft: Symmetrie um den Ursprung
![]() (20)
(20)
Diese Eigenschaft besagt, dass Informationen aus zwei benachbarten Quadranten alle Informationen enthalten, die durch die Kreuz-Ambiguitätsfunktion bereitgestellt werden. Die Informationen in den verbleibenden Quadranten sind redundant. Ein Beweis für die Symmetrieeigenschaft wird im Anhang A präsentiert.
Das Spektrum eines Radar-Signals beeinflusst maßgeblich die Auflösung der Kreuz-Ambiguitätsfunktion. Die Auflösung der Kreuz-Ambiguitätsfunktion von Signalen wie analogen Radiostationen wird durch den Inhalt des Station-Programms beeinflusst. Die ideale Kreuz-Ambiguitätsfunktion wird als Daumennagel-Funktion bezeichnet und hat einen einzelnen Spike am Ursprung. Ein Beispiel für eine Kreuz-Ambiguitätsfunktion, die die ideale Daumennagel-Funktion annähert, ist in Abbildung 4 dargestellt. In dieser Arbeit werden nur zwei Quadranten der Kreuz-Ambiguitätsfunktion gezeigt, da die anderen beiden gemäß der Symmetrieeigenschaft nur redundante Informationen enthalten. Jeder Punkt im Definitionsbereich der Funktion entspricht einer eindeutigen Zielgeschwindigkeit und bistatischen Reichweite. Der Wert der Funktion an jedem Punkt gibt die relative Größe des empfangenen Echos von einem Ziel in einer bestimmten Entfernung und mit einer bestimmten Geschwindigkeit an.
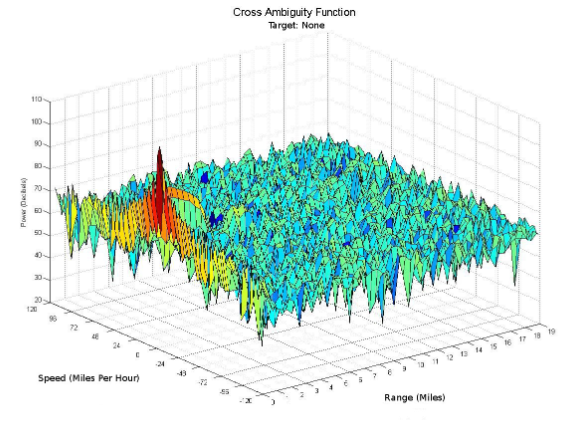
Abb. 4. Beispiel für eine Kreuz-Ambiguitätsfunktion. Dies ist eine Kreuz-Ambiguitätsfunktion, die mit einem Signal berechnet wurde, das bandbegrenztes, gaussches Rauschen aufweist.
Radar signale, die Kreuzambiguitätsfunktionen erzeugen, die die ideale Reißnagel-Funktion approximieren, haben große Bandbreiten und rauschähnliche Eigenschaften. Aufgrund der rauschähnlichen Eigenschaften sind die Frequenzen des Signals nicht miteinander korreliert. Dies führt zu einem schmalen Peak in der Kreuzambiguitätsfunktion, ähnlich wie bei der Kreuzkorrelation. Je besser die Kreuzambiguitätsfunktion eines Signals die ideale Reißnagel-Funktion approximiert, desto besser ist seine Reichweitenauflösung. Die ideale Reißnagel-Kreuzambiguitätsfunktion hat tatsächlich keine Ambiguität. Digitale Fernsehsignale teilen sich beide Eigenschaften unabhängig vom Fernsehprogramm und erzeugen gute Kreuzambiguitätsfunktionen, die eine Reichweitenauflösung von bis zu 20 Metern liefern können [2, 14]. Die Kreuzambiguitätsfunktion des Sendersignals, das in dieser Forschung verwendet wird, ist in Abbildung 5 dargestellt. Ein digitales Fernsehsignal wurde aufgrund seiner Verfügbarkeit, hohen Leistung, großen Bandbreite und rauschähnlichen Eigenschaften ausgewählt, was zu einer Kreuzambiguitätsfunktion führt, die die ideale Reißnagel-Funktion approximiert.
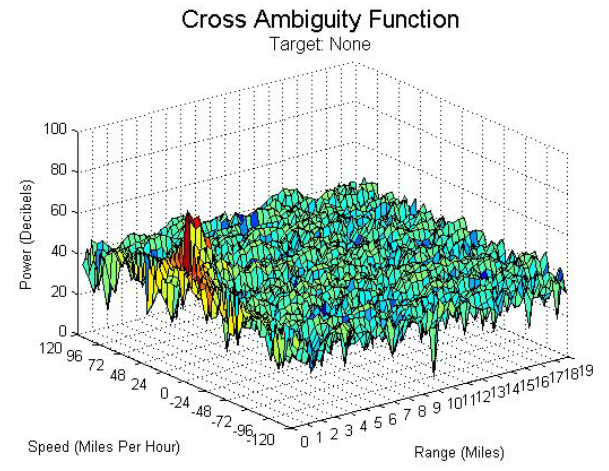
Fig. 5. Kreuz-Ambiguitätsfunktion des digitalen Fernsehsignals. Die Kreuz-Ambiguitätsfunktion des WKNO-Digitalfernsehsignals ohne Zielpräsenz. Wie erwartet für ein breitbandiges, rauschähnliches Signal nähert sich die resultierende Kreuz-Ambiguitätsfunktion der idealen Daumennagelfunktion an.
I. Software-Defined Radio
1. Das Universal Software Radio Peripheral
Das Universal Software Radio Peripheral (USRP) ist ein kostengünstiges Gerät, das mit Software-Defined Radio verwendet wird und Funksignale empfängt und sendet. Das USRP verbindet sich über die USB 2.0-Schnittstelle mit einem Personalcomputer. Das Gerät besteht aus einer Hauptplatine, die Analog-Digital-Wandler (ADC), Digital-Analog-Wandler (DAC), ein programmierbares Gatterfeld (FPGA) und einen USB-Controller enthält. Tochterplatinen sind für das USRP verfügbar und enthalten Hochfrequenz-Frontends, die es ermöglichen, bei den meisten Frequenzen zwischen Gleichstrom (DC) und 5 GHz zu arbeiten.
Die ADCs des USRP werden verwendet, um analoge Signale von einer Antenne in digitale Daten umzuwandeln, die über USB an einen Computer gesendet werden können, um verarbeitet zu werden. Die DACs ermöglichen es dem USRP, digitale Signale von einem Computer in analoge Signale umzuwandeln, die mit einer Antenne ausgestrahlt werden können. Die ADCs und DACs arbeiten mit Abtastraten von 64 MHz bzw. 128 MHz und verwenden komplexe Proben. Dies ermöglicht es empfangenen und gesendeten Signalen, Frequenzen von bis zu 32 MHz bzw. 64 MHz zu enthalten, wobei der Nyquist-Kriterium erfüllt wird. Dieser Prozess wird in Abbildung 6 dargestellt.
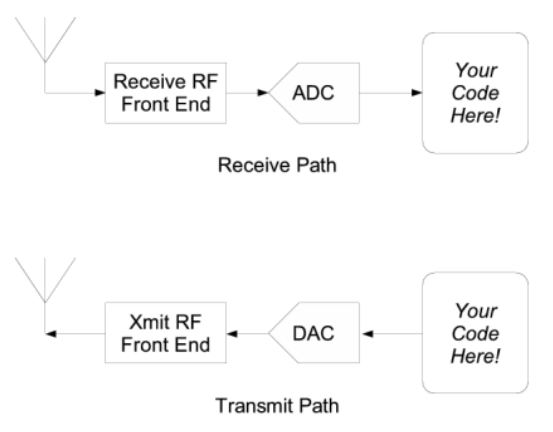
Fig. 6. Software-definiertes Blockdiagramm [15]. Die empfangenen Signale werden vom Frontend des Empfängers verstärkt, heruntergemischt und gefiltert, bevor sie von dem ADC abgetastet und schließlich an einen Computer für allgemeine Zwecke gesendet werden. Der Übertragungspfad ist ähnlich, aber umgekehrt.
Der FPGA ist für die anfängliche Signalverarbeitung verantwortlich, wie zum Beispiel komplexe Mischung und Dezimierung, bevor die Daten vom USRP an den verbundenen Personalcomputer gesendet werden. Die genaue Konfiguration des FPGAs und die Funktionen, die es ausführt, können durch Laden unterschiedlicher Firmware auf das USRP verändert werden, um das FPGA neu zu konfigurieren. Abb. 7 zeigt eine typische FPGA-Konfiguration für den Empfang. In der gezeigten Konfiguration mischt der FPGA Sinuswellen mit den empfangenen Signalen, um sie auf die Basisbandfrequenz herunterzusetzen. Im Gegensatz zu einem physischen Oszillator kann die Frequenz des numerisch gesteuerten Oszillators (NCO) des FPGAs sofort geändert werden, was für Anwendungen, die Frequenzsprünge erfordern, nützlich ist. Die Signale werden dann tiefpassgefiltert, um Aliasing zu verhindern, und schließlich dezimiert, um den Downconversion-Prozess abzuschließen.
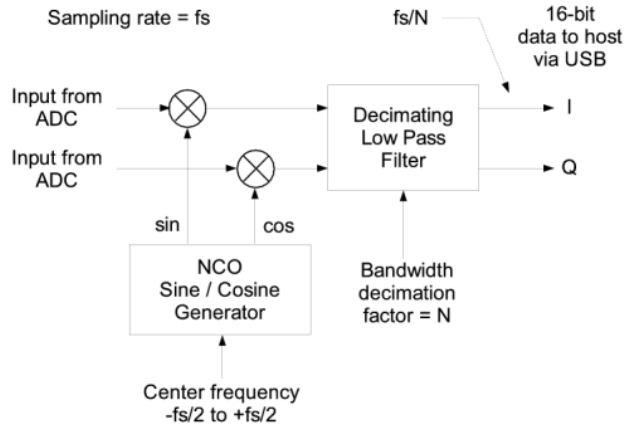
Abb. 7: Ein digitaler Downconverter, implementiert in der FPGA [15]. Digitale Signale von ADCs werden in Quadratur mit Signalen gemischt, die von einem NCO erzeugt werden.
Tochterplatinen sind verfügbar, die als Empfänger, Sender und Transceiver fungieren. Die auf den Karten befindlichen Komponenten umfassen Tuner, Verstärker, Filter, Downconverter und Upconverter. Frequenzumwandlung ist erforderlich, um das Basisbandspektrum in das nutzbare Funkfrequenzspektrum und umgekehrt zu verschieben. Ein Blockdiagramm des USRP einschließlich der Tochterplatinen ist in Abb. 8 dargestellt.
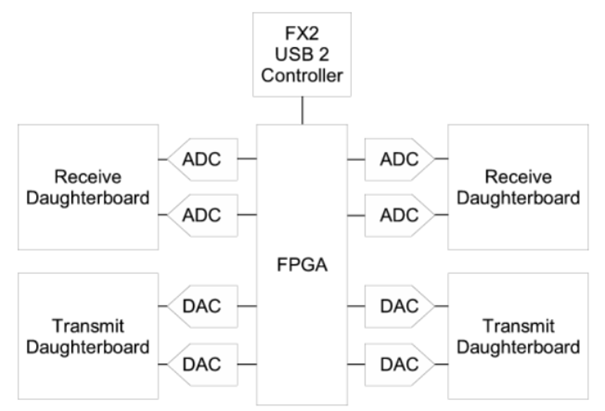
Abb. 8. USRP-Blockdiagramm [15]. Der USRP enthält vier ADCs und vier DACs, was es ihm ermöglicht, gleichzeitig zwei Sender-Tochterplatinen und zwei Empfänger-Tochterplatinen zu unterstützen.
TVRX-Modelle der Tochterplatinen wurden im System verwendet, das in dieser Arbeit präsentiert wird. Die Tochterplatine trägt den Namen TVRX, weil ein Kabelmodem-Tuner als Hochfrequenz-Frontend verwendet wird und daher im ähnlichen Frequenzspektrum wie Kabelfernsehen und Rundfunk arbeitet. Der TVRX-Empfänger wurde ausgewählt, da eine digitale Rundfunkfernsehstation als Beleuchter für das System verwendet wird. Der USRP ist nicht kalibriert. Obwohl der USRP die Messung der relativen Signalstärke ermöglicht, kann die Messung der absoluten Signalgröße ohne Kalibrierung nicht durchgeführt werden. Daher sind alle mit dem USRP gesammelten und in dieser Arbeit präsentierten Daten relativ.
2. GNU Radio
GNU Radio ist ein Open-Source-Software-Toolkit, das in Verbindung mit dem USRP verwendet wird, um softwaredefinierte Radios umzusetzen. GNU Radio besteht aus zahlreichen Software-Blöcken, von denen jeder eine Signalverarbeitungsfunktion implementiert, die traditionell in Hardware umgesetzt wurde. Die Software-Blöcke umfassen Modulatoren, Verstärker, Signalgeneratoren, mathematische Operatoren und so weiter. Um ein hohes Maß an Recheneffizienz zu erreichen, sind die Blöcke in C/C++ geschrieben.
Softwaredefinierte Radios werden mit GNU Radio als Signalflussdiagramme erstellt. Signalverarbeitungsobjekte oder Softwaremodule sind miteinander verbunden, um das Radiosystem zu bilden. Jedes Modul verfügt über Ports, die Signalinputs oder -outputs sein können und die durch die Kanten des Diagramms miteinander verbunden sind, über die Signale übertragen werden. Für die Benutzerfreundlichkeit wird die Hochsprache Python verwendet, um Signalflussdiagramme zu definieren, die aus in C++ geschriebenen Modulen bestehen. Zusätzlich bietet GNU Radio Companion (GRC) eine Benutzeroberfläche zum grafischen Erstellen von Signalflussdiagrammen, indem Python-Code aus vom Benutzer gezeichneten Diagrammen generiert wird.
Ein mit GRC entwickelter softwaredefinierter Breitband-FM-Radioempfänger ist in Abbildung 9 dargestellt. Das Signal vom USRP wird durch das WBFM-Empfangsmodul demoduliert und erzeugt ein Audiosignal, das an die Audio-Schnittstelle des Computers gesendet wird. GNURadio-Softwaremodule werden ausgewählt und als Objekte instanziiert, indem sie aus der Liste im rechten Fensterbereich ausgewählt werden. Rechtecke, die die Objekte repräsentieren, werden im Hauptfensterbereich verschoben und miteinander verbunden, um das Diagramm zu bilden. Parameter wie Verstärkung oder Frequenz für jedes Modul können entsprechend für jedes Modulobjekt spezifiziert werden.
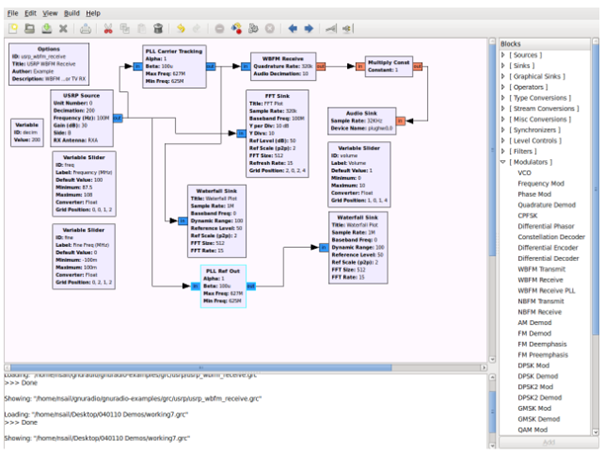
Fig. 9. Die GRC-Benutzeroberfläche. Die GNU Radio-Signalverarbeitungsblöcke können grafisch konfiguriert und verbunden werden. Der spezielle Graph, der hier gezeigt wird, implementiert einen Breitband-FM-Radioempfänger.
3. Experimentelle Systemanalyse und Implementierung
A. Systemempfindlichkeit
Damit die Detektion von Flugzeugen möglich ist, muss der Empfänger unter idealen Bedingungen zumindest in der Lage sein, Echo-Signale zu erkennen. Das bedeutet, dass eine günstige Geometrie vorliegen muss und das Flugzeug gut beleuchtet und orientiert ist, so dass das Radar-System einen großen Radarquerschnitt beobachtet. Um die Detektion dieser Signale zu erwarten, sollte die vorhergesagte Signalstärke, wie in Gleichung (11) gefunden, größer sein als die theoretisch minimale detektierbare Leistung. Unter der Annahme, dass der TVRX-Empfänger einen Rauschfaktor von 8 dB hat [16], kann seine minimale detektierbare Signalstärke mit Gleichung (16) berechnet werden.
![]() (21)
(21)
Daher wird nicht erwartet, dass der Empfänger Signale schwächer als -98 dBm von der Antenne erfassen kann.
Die minimal nachweisbare Signalstärke wurde von uns experimentell bestimmt, indem wir einen kalibrierten variablen Leistungssignalgenerator verwendet haben, der auf die interessierende Frequenz abgestimmt wurde.
Das Signal des Signalgenerators wurde direkt über ein kurzes koaxiales Kabel in den USRP eingespeist. Die Fourier-Transformation dieses Signals wurde in Echtzeit durchgeführt und dargestellt, während die Leistung des Signals abnahm. Die minimal nachweisbare Leistung wurde als die Leistung betrachtet, die vom Signalgenerator angezeigt wurde, wenn die Leistung so verringert wurde, dass das Signal nicht mehr beobachtbar war. Die vom Signalgenerator angezeigte Leistung wurde durch Anschließen des Signalgenerators an einen Spektrumanalysator bestätigt und gemessen. Die minimal nachweisbare Leistung wurde experimentell auf etwa -80 dBm gemessen.
B. Illuminator
Als Illuminator wurde eine digitale Fernsehstation ausgewählt, da digitale Fernsehsender weit verbreitet, leistungsstark und mit einer wünschenswerten Kreuzambiguitätsfunktion ausgestattet sind. Die für das hier vorgestellte System verwendete Fernsehstation mit dem Rufzeichen WKNO in Memphis, Tennessee, hat eine Trägerfrequenz von 560,31 MHz und eine entsprechende Wellenlänge von 0,535 m. Das Spektrum des Signals von WKNO ist in Abbildung 10 dargestellt.
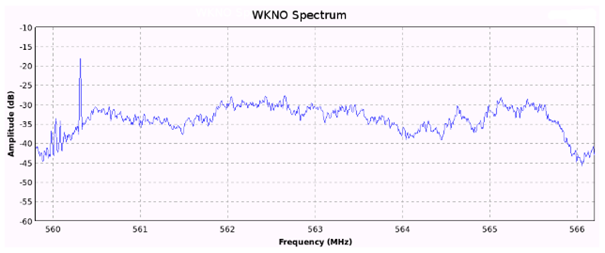
Fig. 10. Spektrum von WKNO. Das Signal von WKNO nimmt das Frequenzspektrum zwischen 560 MHz und 566 MHz ein. Der Träger lässt sich leicht bei 560,31 MHz identifizieren.
C. Vorläufige Systemkonfigurationen
Das System wurde zunächst als ein einzelner Empfänger mit einer omnidirektionalen Viertelwellen-Dipolantenne konfiguriert. Mit dieser Konfiguration sollte es möglich sein, Dopplerschübe durch bewegte Objekte zu detektieren. Die Untersuchung solcher Dopplerschübe wurde durch die Beobachtung von Spektrogrammen des empfangenen Signals durchgeführt.
Ein ideales Signal für diese Art von Analyse ist eines, das in der Nähe ausgestrahlt wird, leistungsstark ist und einen schmalen Träger hat, der sich nicht in der Frequenz ändert. Das bedeutet, dass ein amplitudenmoduliertes (AM) Signal einem frequenzmodulierten (FM) Signal vorgezogen wird. Es wurden nur Signale in Betracht gezogen, die kontinuierlich ausgestrahlt wurden.
Niedrigfrequente Signale, wie das AM-Radio-Band von 535 kHz bis 1705 kHz, erwiesen sich als ungeeignet, da die Dopplerfrequenzen nicht weit genug vom Träger verschoben wurden, um eine zuverlässige Detektion zu ermöglichen. Analoges Fernsehsignal schien vielversprechend, jedoch wurden zum Zeitpunkt dieser Forschung hochleistungsfähige analoge Fernsehsignale kürzlich durch digitale Signale ersetzt.
D. Testziel
Ein Ventilator wurde als Ziel für Tests des Systems in einem Laborumfeld verwendet. Das Ventilatorziel und die Yagi-Antenne, die für diese Forschung verwendet wurden, sind in Abbildung 11 dargestellt. Die sich bewegenden Ventilatorblätter bieten ein schnell bewegliches, variable Geschwindigkeit Ziel, das für Tests des Systems im Labor verwendet werden kann. Die Doppler-Signatur eines rotierenden Flügels ist gut erforscht und leicht erkennbar [17].

Abb. 11. Testziel und Zielantenne. Ein als Testziel verwendeter Ventilator ist dargestellt,
mit einer Yagi-Antenne, die mit dem Zielkanal verbunden ist. Die Antenne, montiert
auf einem Stativ, ist aus Kunststoffrohren und Metallstangen gefertigt.
E. Vorhergesagte Empfangsleistung des Echosignals
Die bistatische Radar-Gleichung (11) kann verwendet werden, um die Leistung der Echosignale vorherzusagen, die vom experimentellen System empfangen werden. Die Radar-Gleichung wurde unter Verwendung von Werten berechnet, die dem in dieser Forschung verwendeten System entsprechen. WKNO sendet mit einer Leistung von 835 kW über eine Antenne mit 14 dB Gewinn. Der General DeWitt Spain Airport, ein Datensammelort für dieses Projekt, befindet sich 22 km vom Sender von WKNO entfernt. Eine typische Radarkreuzung wurde ausgewählt, indem ein Wert aus Abb. 2 ausgewählt wurde. Die 12-dB-Antenne des Radarempfängers wurde in weniger als 1 km Entfernung von den Enden der Startbahn aufgestellt, daher wurde 1 km als Ziel-zu-Empfänger-Entfernung ausgewählt. Die Trägerfrequenz von WKNO beträgt 560,31 MHz, was einer Wellenlänge von 0,535 m entspricht. Die Berechnung wurde wie folgt durchgeführt:
Sendeleistung Pt = 835 kW
Sendenantennengewinn Gt = 14 dB
Sender-zu-Ziel-Entfernung r1 = 22 km
Ziel-bistatische Radarkreuzung σb = 20m2
Ziel-zu-Empfänger-Entfernung r2 = 1 km
Empfangsantennengewinn Gr = 12 dB
Radawellenlänge λ = 0,535 m
resultierend in
![]() (22)
(22)
Die vorhergesagte Leistung von -57 dBm ist deutlich höher als das theoretische Minimum von -98 dBm. Obwohl diese Vorhersage von einem bestmöglichen Szenario ausgeht, ist das Ergebnis ermutigend.
F. Senderantennenmuster
Die Antennenmuster für den Sender wurden in den späten Phasen dieser Forschung erfasst und gaben einige Einblicke in die Schwierigkeiten, die mit dem System auftraten. Wie in der Abbildung 12 durch das Antennenmuster dargestellt, ist die vertikale Strahlbreite der Antenne sehr schmal und in Richtung Boden geneigt. Die Daten in Tabelle 1 zeigen eine vertikale Strahlbreite von nur etwa 2 Grad.
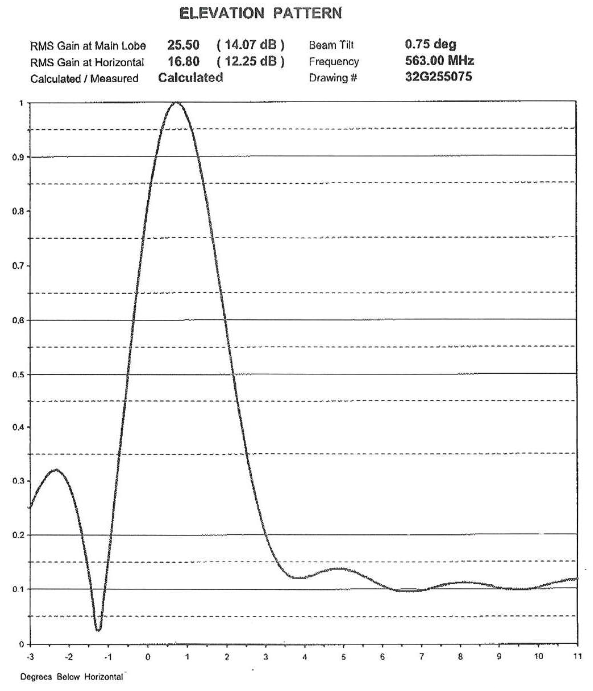
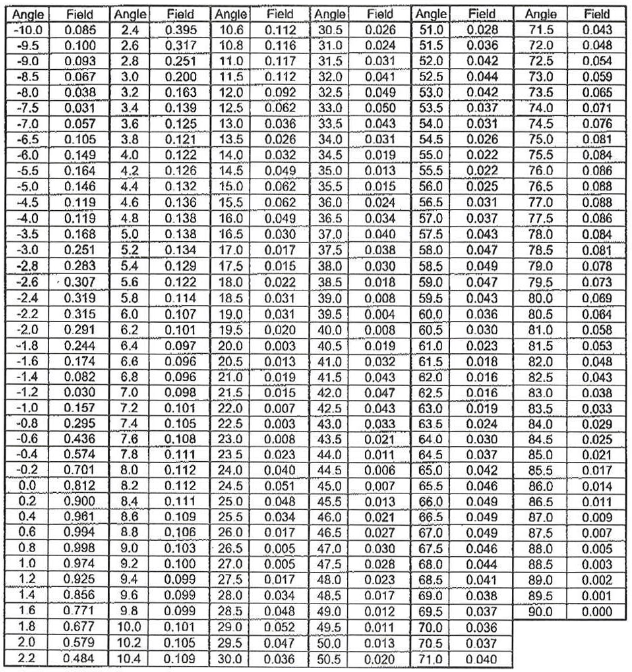
Abb. 12. Vertikales Antennenmuster für die Senderantenne [18]. Der Strahlungsbereich der Senderantenne hat eine vertikale Halbwertsbreite von nur etwa 2 Grad und ist um 0,75 Grad nach unten geneigt. Die Strahlbreite wurde nicht so schmal erwartet.
Tabelle 1. Höhenmuster-Tabelle für die Senderantenne [18]. Die Werte in dieser Tabelle wurden in Abbildung 12 verwendet. Der untere Rand des Strahls liegt etwa 1,6 Grad unter der Horizontalen, und der obere Rand liegt etwa 0,2 Grad über der Horizontalen.
Die schmale, nach unten geneigte Antennenstrahlung führt dazu, dass nur Flugzeuge in extrem niedrigen Höhen gut beleuchtet werden. Abbildung 13 zeigt, wie die schmale vertikale Strahlbreite des Senders die Höhe begrenzte, in der Flugzeuge erkannt werden konnten. Selbst 22 km entfernt vom Sender am General DeWitt Spain Airport liegt die Spitze des Strahls nur 77 m über der Antenne in einer Höhe von 311 m, von der er stammt. Dies führt dazu, dass nur Flugzeuge, die unter 388 m fliegen, gut beleuchtet werden. Die extreme Schmalheit der Strahlbreite war zu Beginn dieser Forschung nicht bekannt und wird weitgehend für die erheblichen und unerwarteten Schwierigkeiten bei der Erkennung von Flugzeugen in moderat hohen Höhen verantwortlich gemacht.
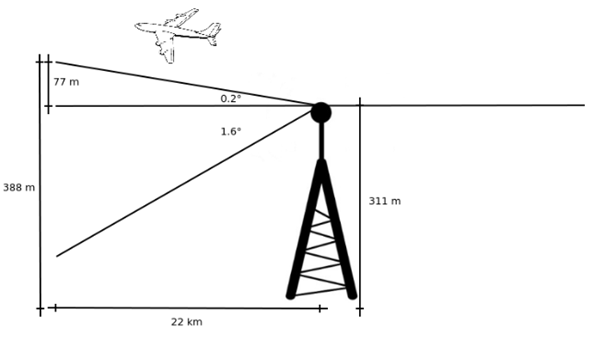
Abb. 13. Flugzeug über Strahl. Diese Diagramm veranschaulicht, warum Flugzeuge in großer Höhe nicht gut beleuchtet sind.
4. Experimentelle Ergebnisse
A. Laboruntersuchungen
Das Lüfterziel wurde ausgiebig für Tests und zur Validierung des Systems verwendet. Während der frühen Forschung wurde die Bestätigung einer Doppler-Signatur durch die Verwendung eines einzelnen Kanals zur Datensammlung gesucht. Eine omnidirektionale Antenne, die mit dem einzelnen Kanal verbunden war, wurde in der Nähe der sich drehenden Lüfterblätter positioniert.
Bei Verwendung einer omnidirektionalen Antenne auf einem einzelnen Kanal wurde der Lüfter nicht zuverlässig erkannt. Neben dem gewünschten Echo empfing die omnidirektionale Antenne auch das Direktpfad-Signal. Da digitale Fernsehsignale ein breites, rauschähnliches Spektrum haben, wirkte das Direktpfad-Signal wie ein hoher künstlicher Rauschpegel, der das Erkennen von Doppler-Seitenbändern verhinderte.
Um die Doppler-Verschiebungen im Zielsignal zu erkennen, war es notwendig, das Zielsignal vom Direktpfad-Signal zu isolieren. Eine 10-Element-Yagi-Antenne mit einer theoretischen Verstärkung von 12 dB wurde konstruiert, wie in Abbildung 11 gezeigt. Nachdem diese Antenne mit dem einzelnen Kanal verbunden wurde, war die Detektion der Doppler-Signatur des Lüfters möglich. Abbildung 14 zeigt ein Diagramm des empfangenen Spektrums unter Verwendung der Hochgewinnantenne. Die Doppler-Verschiebungen sind bei -75 Hz und 75 Hz deutlich sichtbar. Die positive Doppler-Verschiebung wird durch Echos von vorrückenden Blattoberflächen verursacht, während die negative Doppler-Verschiebung durch sich zurückziehende Blattoberflächen verursacht wird. Diese Doppler-Verschiebungen entsprechen einer Lüfterblattgeschwindigkeit von etwa 90 MPH.
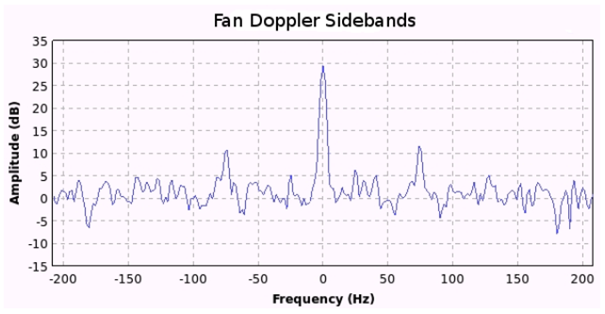
Fig. 14. Doppler-Seitenbänder eines Lüfterziels. Die durch eine rotierende Lüfterklinge verursachten Dopplerverschiebungen werden auf jeder Seite des Trägers dargestellt.
Um festzustellen, ob die mit dem Doppler-Effekt gemessene Geschwindigkeit der Lüfterblätter vernünftig war, wurde die Geschwindigkeit auch durch Analyse des vom Lüfter emittierten Geräuschs gemessen. Das Audiosignal wurde von einem Mikrofon in der Nähe des Lüfters aufgenommen. Ein Spektrogramm des Audiosignals ist in Abbildung 15 dargestellt. Die grundlegende harmonische Frequenz wurde bei 76 Hz gefunden, was einer Winkelgeschwindigkeit von 1523 U/min entspricht. Unter Verwendung des Durchmessers des Lüfters von 19,5 Zoll wird die Geschwindigkeit der Flügelspitzen auf etwa 88 Meilen pro Stunde geschätzt, was in enger Übereinstimmung mit der Doppler-Messung von 90 Meilen pro Stunde liegt.
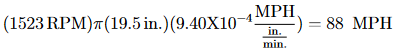
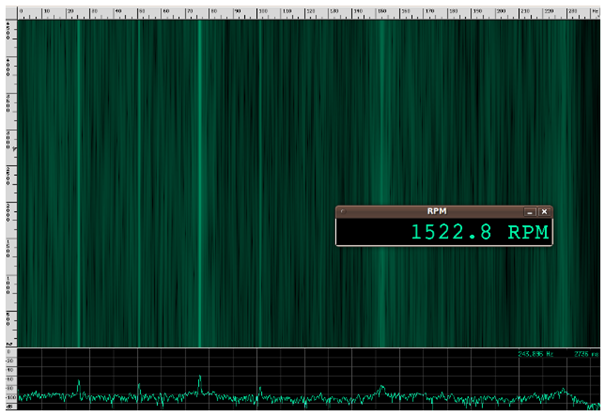
Abb. 15. Akustisches Spektrogramm des Ventilators. Zur Vergleichbarkeit mit der Doppler-Messung der Geschwindigkeit der Ventilatorblätter wurde das Spektrum des vom Ventilator abgegebenen Geräusches analysiert. Diese Analyse und die Doppler-Geschwindigkeitsmessung lieferten nahezu identische Messergebnisse.
Das Spektrogramm in Abbildung 16 zeigt, wie sich das Doppler-Spektrum verändert, wenn sich die Geschwindigkeit eines Ziels ändert. Das Ziel ist ein sich startender und stoppender Ventilator, und es wird nur ein einzelner Radioreceiver und eine Antenne verwendet. Die vertikale Linie bei null Hertz ist der Träger des digitalen Fernsehsignals. Die durch die sich bewegenden Ventilatorblätter verursachte Dopplerverschiebung ist auf beiden Seiten des Trägers zu erkennen. Die Ventilatorblätter beginnen sich zwischen 10 und 30 Sekunden zu drehen und zu beschleunigen. Zwischen 30 und 50 Sekunden dreht sich der Ventilator mit konstanter Geschwindigkeit und verursacht eine Dopplerverschiebung von etwa 75 Hz. Etwa bei 50 Sekunden wird der Ventilator ausgeschaltet, und die Ventilatorblätter beginnen langsam abzubremsen. Ohne Abzug eines Referenzsignals vom Zielsignal ist die direkte Pfadinterferenz sehr deutlich.
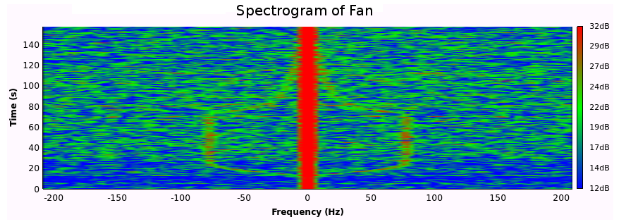
Abb. 16. Spektrogramm eines Ventilators beim Starten und Stoppen ohne Verwendung eines Referenzkanals. Die vertikale Linie bei null Hertz repräsentiert das Trägersignal des digitalen Fernsehsignals. Der durch die sich bewegenden Ventilatorblätter verursachte Dopplerverschiebungseffekt ist auf beiden Seiten des Trägersignals zu erkennen.
Trotz der Verbesserungen durch die Yagi-Antenne war das System immer noch nicht in der Lage, tieffliegende Flugzeuge über dem Campus der University of Memphis zu erkennen. Nachdem keine zufriedenstellenden Ergebnisse bei der Datensammlung auf dem Universitätsgelände erzielt werden konnten, wurde das System am General DeWitt Spain Airport aufgestellt, um Daten von startenden und landenden Flugzeugen zu sammeln. Der General DeWitt Spain Airport befindet sich 22 km entfernt vom WKNO-Sendestandort, wie in Abb. 17 gezeigt.
Das System wurde 120 m seitlich von der Mitte der Start- und Landebahn positioniert, wobei die Yagi-Antenne auf die An- und Abflugwege der Flugzeuge ausgerichtet war. Eine Luftaufnahme der Anordnung ist in Abb. 18 zu sehen. Mit dieser Konfiguration wurden viele Datensätze gesammelt und analysiert. Trotz der Nähe zu diesen tieffliegenden Flugzeugen wurden keine Doppler-Signaturen in den Daten gefunden.
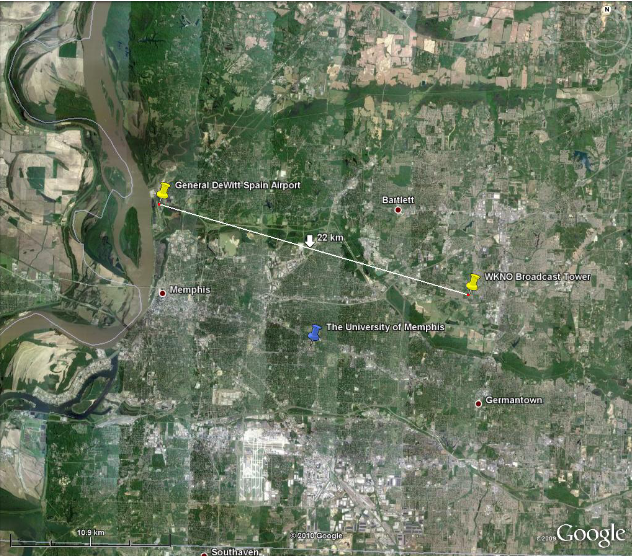
Fig. 17. Luftaufnahme des Systems [19]. General DeWitt Spain befindet sich 22 km nordwestlich des Sendestandorts von WKNO.

Abb. 18. Luftaufnahme des Sammelorts am Flughafen [19]. Das System wurde eingerichtet und die Daten wurden 120 m seitlich vom Mittelpunkt der Landebahn gesammelt. Ein ähnliches System [1] verwendete einen zweiten Empfänger und eine gerichtete Antenne zur zusätzlichen Isolierung des Direktpfad-Signals. Die zweite Antenne war auf den Sender ausgerichtet, um nur das Direktpfad-Signal zu empfangen. Der Kanal, der das Direktpfad-Signal empfängt, oder der Referenzkanal, wurde vom Zielkanal abgezogen, um mehr vom Direktpfad-Signal aus dem Zielkanal zu entfernen. Das Ergebnis dieser Kanal-Subtraktion wurde zusammen mit dem Signal des Referenzkanals verwendet, um die Kreuzambiguitätsfunktion zu berechnen.
Um denselben Typ der Entfernung des Direktpfad-Signals zu implementieren, wurde ein zweites TVRX-Empfangsmodul zum USRP hinzugefügt, und eine zweite identische Yagi-Antenne wurde konstruiert. Jedes TVRX-Modul hat seinen eigenen lokalen Oszillator, der nicht mit dem anderen synchronisiert ist. Ohne Synchronisation der lokalen Oszillatoren wäre das System nicht mehr kohärent. Da die Synchronisation der lokalen Oszillatoren nicht möglich war, wurde eine Möglichkeit zur Synchronisierung der Signale in der Software mit GNU Radio entwickelt.
B. Abschließende Systemkonfiguration
GNU Radio enthält einen phasenverriegelten Schleifen-(PLL) Trägerverfolgungsblock. Mithilfe eines PLL sperrt der Block die Trägerfrequenz des digitalen Fernsehsignals und verschiebt das Spektrum des Signals so, dass der Träger bei null Frequenz liegt. Die Ziel- und Referenzkanäle werden durch PLL-Trägerverfolgungsblöcke geleitet, um ihre Spektren auszurichten. Dies korrigiert mögliche Unterschiede in den Frequenzen, auf die die Empfänger abgestimmt sind, die durch Unterschiede in ihren Frequenzreferenzen verursacht werden.
Nachdem die Spektren ausgerichtet sind, wird die Phase jedes Signals berechnet, und die Phase des Ziel-Signals wird von der Phase des Referenz-Signals subtrahiert, um einen relativen Phasenunterschied zwischen den beiden Signalen zu erhalten. Dieser Unterschied wird durch einen Phasenmodulator geschickt, und das resultierende Signal wird mit dem frequenzangepassten Ziel-Signal multipliziert, um den Phasenunterschied zu entfernen und das System kohärent zu machen. Der Prozess ist in Abbildung 19 dargestellt.
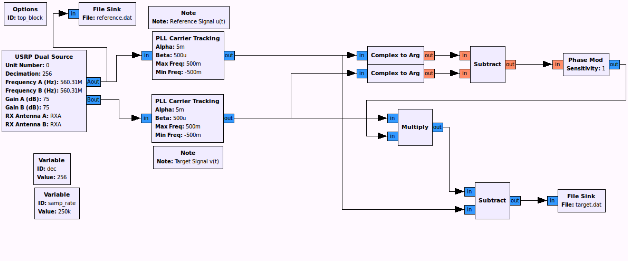
Abb. 19. Blockdiagramm des Datenerfassungsprozesses. Referenz- und Zielkanalsignale stammen aus dem USRP-Quellblock. PLL-Blöcke verwenden die Trägerfrequenz als Referenz, um beide Kanäle auf die gleiche Frequenz feinzutunen. Der Phasenunterschied zwischen den Signalen wird berechnet und zur Anpassung der Phase des Zielsignals verwendet, sodass es phasenkohärent mit dem Referenzsignal ist.
Nach der Kohärenzbildung des Systems wurde das Zwei-Kanal-System mit dem Ventilator als Ziel getestet. Die Antenne des Zielkanals war auf den Ventilator gerichtet, während die Antenne des Referenzkanals in Richtung des Senders ausgerichtet war. Das Spektrogramm in Abb. 20 zeigt im Vergleich zur Ein-Kanal-Konfiguration eine deutliche Verbesserung. Der Träger wurde nahezu vollständig entfernt.
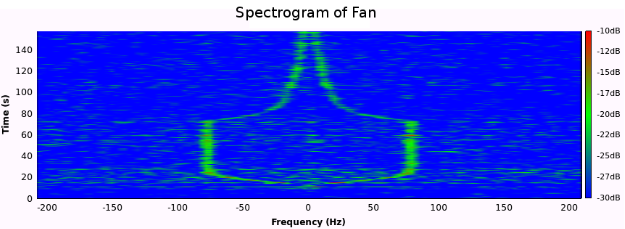
Fig. 20. Spektrogramm eines Ventilators beim Starten und Stoppen unter Verwendung eines Referenzkanals. Der Ventilator wird auf die gleiche Weise gestartet und gestoppt wie in Abb. 16 gezeigt. Die Daten, mit denen dieses Spektrogramm erstellt wurde, wurden verarbeitet, indem das Signal des Referenzkanals vom Signal des Zielkanals subtrahiert wurde.
Unter Verwendung von Zwei-Kanal-Daten wurde die Kreuzunsicherheitsfunktion für den Ventilator berechnet und ist in Abbildung 21 dargestellt. Alle in dieser Arbeit präsentierten Daten wurden mit einer Abtastrate von 250 Kilosamples pro Sekunde erfasst, was einer Abtastperiode von 4 μs entspricht. Während einer Abtastperiode legt das Signal (4 μs)c zurück, was einer Hin- und Rückreisedistanz von 1,2 km und einer Reichweite von 600 m entspricht. Dies begrenzt die Reichweitenauflösung der Kreuzunsicherheitsfunktion auf etwa 600 m, da das Signal mindestens eine Abtastperiode verschoben wird, wenn die CAF berechnet wird. Alle mit dem System beobachteten und hier präsentierten Ziele befanden sich innerhalb von 600 m und erscheinen daher im Bereichsintervall der Kreuzunsicherheitsfunktion von null m bis 600 m.
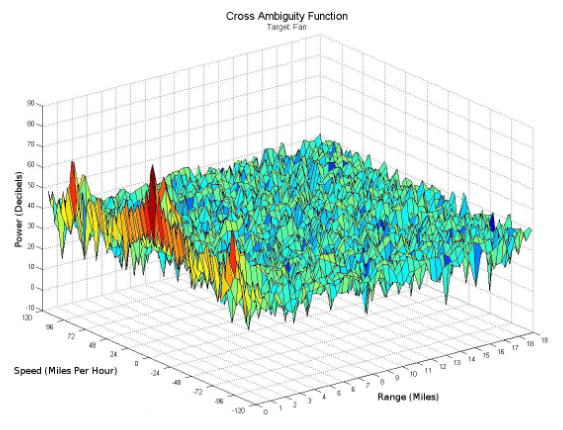
Abb. 21. Kreuzambiguitätsfunktion bei Vorhandensein des Ventilatorziels. Die beiden gleichmäßig vom Ursprung entfernten Spitzen repräsentieren die sich bewegenden Ventilatorblätter.
C. Flughafendaten
Das Zweikanalsystem wurde am Flughafen an derselben Position wie das Einkanalsystem gemäß Abbildung 18 aufgebaut. Die Daten wurden auf dieselbe Weise wie beim Einkanalsystem gesammelt, mit dem Unterschied, dass die neue Referenzantenne vorhanden war und auf den Sender ausgerichtet war. Abbildung 22 zeigt die endgültige Systemkonfiguration, die am Flughafen eingerichtet wurde. Mehrere Datensätze wurden für verschiedene Flugzeuge unter Verwendung dieser Konfiguration gesammelt. In diesen Daten wurde eine Doppler-Signatur für ein startendes Flugzeug gefunden.

Abb. 22. System am Flughafen. Das System befand sich 120 m von der Startbahn entfernt. Die Referenzantenne war auf die Fernsehsendeanlage ausgerichtet, während die Zielantenne in Richtung des Pfads ausgerichtet war, den Flugzeuge für Starts und Landungen nutzen.
Die Daten wurden direkt von der USRP ohne zusätzliche Verarbeitung aufgezeichnet. Der Kohärenzprozess in Abbildung 19 wurde während der späteren Verarbeitung durchgeführt. Die kohärenten Daten wurden schließlich mit MATLAB verarbeitet, um die Kreuzambiguitätsfunktion zu berechnen.
Um zu sehen, wie sich der Dopplerverschiebung des Flugzeugs im Laufe der Zeit beim Start entwickelte, wurden die Daten in Zeitintervalle aufgeteilt, und der Null-Range-Bin der Kreuzambiguitätsfunktion wurde für jeden berechnet. Die Ergebnisse dieser Berechnungen wurden entlang der Frequenzachse als Reihen dargestellt, um ein Diagramm ähnlich einem Spektrogramm zu erstellen. Der Unterschied besteht darin, dass der Null-Range-Bin der Kreuzambiguitätsfunktion anstelle der STFT verwendet wurde.
Das resultierende Diagramm ist in Abbildung 23 dargestellt. Eine Doppler-Signatur, die mit dem Passieren des Flugzeugs am Standort des Radarsystems übereinstimmt, ist zu sehen. Das Diagramm ist symmetrisch zur vertikalen Achse, weil die Kreuzambiguitätsfunktion entlang des Null-Range-Bins symmetrisch ist, und dieses Diagramm besteht nur aus Daten des Null-Range-Bins. In den ersten beiden Sekunden nähert sich das Flugzeug der Radarantenne, die sich in der Mitte der Startbahn befindet. Bei 3 Sekunden passiert das Flugzeug die Antenne, und es wird keine Dopplerverschiebung erkannt, weil die radiale Komponente der Fluggeschwindigkeit null ist. Nach 3 Sekunden gewinnt das Flugzeug weiter an Geschwindigkeit, und die radiale Geschwindigkeit nimmt zu, was zu einer zunehmenden Dopplerverschiebung führt. Das Diagramm ist symmetrisch zur vertikalen Achse, weil die Kreuzambiguitätsfunktion entlang ihres Ursprungs symmetrisch ist. Wenn sich das Flugzeug nicht innerhalb von 600 m befunden hätte, wäre nur eine Seite der Doppler-Signatur gleichzeitig vorhanden gewesen, und sie hätte die Null-Geschwindigkeitslinie bei 3 Sekunden gekreuzt. Die Geschwindigkeitsachse wurde mit (17) skaliert. Da der Winkel α kontinuierlich wechselt und unbekannt ist, wurde angenommen, dass er null ist. Diese Annahme führt zu einer gewissen Unterschätzung der Geschwindigkeit.
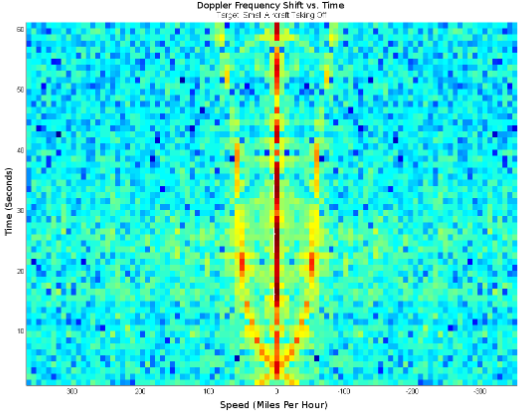
Abb. 23. Kreuz-Ambiguitätsfunktion bei null Entfernungsüberlappung im zeitlichen Verlauf für den Start eines Flugzeugs. Die Kreuz-Ambiguitätsfunktion wurde nur für den Bereich null Entfernungsüberlappung im zeitlichen Verlauf berechnet.
Die Kreuzambiguitätsfunktion, die um den 52-Sekunden-Markierungspunkt der in Abbildung 23 gezeigten Daten berechnet wurde, ist in Abbildung 24 dargestellt. Die Doppler-Signatur zeigt sich als symmetrische Spitzen im Null-Bereichs-Bin, wie erwartet.
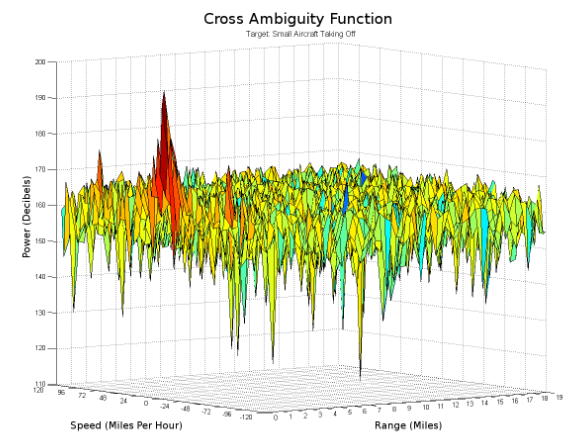
Fig. 24. Kreuzambiguitätsfunktion bei Anwesenheit eines Flugzeugs. Die Kreuzambiguitätsfunktion wurde für ein Flugzeug unter Verwendung der Daten aus Abbildung 23 auf Seite 42 berechnet. Die verwendeten Daten stammen etwa aus der 52-Sekunden-Marke. Zwei Spitzen sind zu sehen, die das Flugzeug repräsentieren.
5. Fazit
Diese Arbeit hat gezeigt, dass ein passives Radarsystem mithilfe von SDR (Software Defined Radio) umgesetzt werden kann, indem ein herkömmliches digitales Fernsehsignal und eine minimale Menge an Hardware verwendet werden. Obwohl mit diesem System die Detektion von Flugzeugen möglich war, müssen mehrere Probleme gelöst werden, bevor praktische Systeme umgesetzt werden können.
Die Verfügbarkeit eines geeigneten Signals stellt vielleicht das größte Hindernis für ein passives Radarsystem dar. Obwohl das für diese Forschung gewählte Signal zunächst aufgrund seiner großen Bandbreite und hohen Leistung ideal schien, stellte sich später heraus, dass die schmale Antennenstrahlbreite des Senders nur sehr niedrig fliegende Flugzeuge beleuchtete. Mit Ausnahme der Antennen des Systems, die für den Empfang bei einer bestimmten Frequenz gebaut wurden, kann das System leicht umkonfiguriert werden, um einen anderen Sender zu verwenden. Andere digitale Fernsehsender in derselben Region wurden gefunden, die etwas wünschenswertere Antennenmuster hatten, wurden jedoch aufgrund von Zeitbeschränkungen und der Notwendigkeit, neue Antennen für diese Frequenzen zu bauen, nicht ausprobiert. Diese Forschung hat deutlich gemacht, wie wichtig die Muster der Senderantennen für passives Radar sind und dass Antennenmuster frühzeitig bei der Implementierung eines Systems berücksichtigt werden sollten.
Störungen durch Direktpfadsignale stellen ein weiteres herausforderndes Problem bei passivem Radar dar. Die Verwendung eines zweiten Empfängers und einer Antenne zur Aufnahme des gesendeten Signals und dessen Subtraktion vom Zielkanal war mäßig erfolgreich bei der Minderung solcher Störungen. Neben dieser Methode könnten adaptive Filteransätze eine verbesserte Entfernung von Direktpfadsignalen ermöglichen.
Die Entwicklung von rechenleistungseffizienten Algorithmen wird ein Schlüsselschritt sein, um Systeme wie dieses praktikabel zu machen. Um Kosten- und Energiebeschränkungen zu erfüllen, benötigen in großen Mengen an abgelegenen Orten bereitgestellte passive Radarsysteme effiziente Software, die in Echtzeit auf langsameren, kostengünstigeren und energieärmeren Prozessoren als denen in Personalcomputern ausgeführt werden kann. Die in dieser Forschung verwendeten Algorithmen waren nicht für solche Einschränkungen optimiert, und es wird erwartet, dass in diesem Bereich erhebliche Verbesserungen möglich sind.
Es wird angenommen, dass eine große Anzahl dieser Systeme entlang ausgedehnter und dünn besiedelter Landesgrenzen platziert werden könnte, um Warnungen vor niedrig fliegenden Flugzeugen zu geben, die die Grenze überqueren. Die Systeme könnten Teil eines größeren Netzwerks von Sensoren werden, die andere Grenzbedrohungen überwachen. Da SDR leicht umkonfiguriert werden kann, könnte dieselbe Hardware, die für das Radar verwendet wird, auch für die Kommunikation im Sensorsystemnetzwerk verwendet werden. SDR würde es auch ermöglichen, die Systeme ferngesteuert zu verbessern und umzukonfigurieren, ohne teure Hardware aufrüsten zu müssen.
Referenzen
1. C. Zoeller, M. J. Budge und M. Moody, "Demonstration des passiven kohärenten Ortungsradars", in "Systemtheorie, 2002. Proceedings des Dreißigsten Südöstlichen Symposiums" (2002), S. 358–362.
2. M. Skolnik, Radar-Handbuch, Dritte Auflage (McGraw-Hill Professional, 2008), Kap. Bistatisches Radar, S. 23.1–23.36.
3. R. C. Watson, Jr., Radar Origins Worldwide: Geschichte seiner Entwicklung in 13 Nationen bis zum Zweiten Weltkrieg (Trafford, 2009).
4. E. Knott, Radarquerschnitt (Westview, Boulder, 1985).
5. P. Howland, D. Maksimiuk und G. Reitsma, "FM-Radio-basiertes bistatisches Radar", Radar, Sonar und Navigation, IEE Proceedings - 152, 107–115 (2005).
6. J. Whitaker, Fernsehempfänger (University of Chicago Press, Chicago, 2001).
7. W. Stutzman, Antennentheorie und -design (Westview, Boulder, 1981).
8. T. Marshall, "Antennen verbessern WLAN-Sicherheit", http://www.trevormarshall.com/byte_articles/byte1.htm (2001).
9. J. DiFranco, Radar Detection (Prentice-Hall, Englewood Cliffs, N.J., 1968).
10. Wikipedia, "Radarquerschnitt — Wikipedia, die freie Enzyklopädie", http://en.wikipedia.org/w/index.php?title=Radar_cross-section&oldid=369978258 (2010).
11. M. Cherniakov, Bistatisches Radar (Harper Perennial, New York, 2008), Kap. Passive bistatische Radarsysteme, S. 247–313.
12. Wikipedia, "Kurzzeit-Fourier-Transformation — Wikipedia, die freie Enzyklopädie", http://en.wikipedia.org/w/index.php?title=Short-time_Fourier_transform&oldid=351474009 (2010).
13. N. Levanon und E. Mozeson, Radar Signals (Wiley-IEEE Press, 2004).
14. R. Saini, M. Cherniakov und V. Lenive, "Unterdrückung von Direktweginterferenzen im bistatischen System: DTV-basiertes Radar", in "Radar Conference, 2003. Proceedings of the International" (2003), S. 309–314.
15. E. Blossom, "GNU Radio erkunden", http://www.gnu.org/software/gnuradio/doc/exploring-gnuradio.html (2004).
16. "Tx- und Rx-Tochterplatinen für das USRP-Software-Radiosystem", http://www.ettus.com/downloads/ettus_ds_USRP_TXRX_v5b.pdf
17. B. Bullard und P. Dowdy, "Puls-Doppler-Signatur eines Drehflügelflugzeugs", Aerospace and Electronic Systems Magazine, IEEE 6, 28–30 (1991).
18. "FCC-Datenbank - Anhang B - Vertikales Elevationsmuster", https://licensing.fcc.gov/cdbs/CDBS_Attachment/getattachment.jsp?appn=101134323&qnum=5070©num=1&exhcnum=3 (2006).
19. Google Earth, "Luftaufnahme und Karte von Memphis, Tennessee", http://earth.google.com
20. C.-Y. Chen und P. Vaidyanathan, "Eigenschaften der MIMO-Radar-Ambiguitätsfunktion", in "Akustik, Sprache und Signalverarbeitung, 2008. ICASSP 2008. IEEE International Conference on" (2008), S. 2309–2312.
A. Nachweis der Symmetrieeigenschaft der Kreuzambiguitätsfunktion
Die Kreuzambiguitätsfunktion ist definiert als
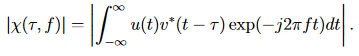 (23)
(23)
Die Symmetrieeigenschaft der Kreuzambiguitätsfunktion besagt [13, 20]
![]() (24)
(24)
Setzt man τ = −τ und f = −f, ergibt sich
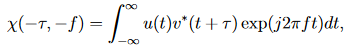
und durch die Änderung der Variable t1 = t + τ ergibt sich
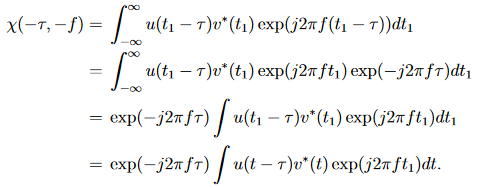
Integration ist eine lineare Operation, daher bleibt die Gleichheit erhalten, indem man den Integranden und das Integrationsresultat konjugiert.
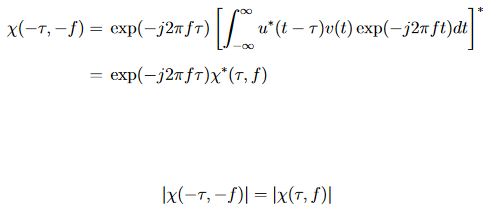 (25)
(25)
